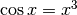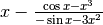CS 2120: Class #6¶
Reusing variables¶
Consider this code fragment:
a = 5 print a b = 6 print a a = a+b print a a = 3 a = a+1 print a
Very Quick Activity
What is the value of the variable a at the various print statements in
the above code?
A very common pattern we’ll use is incrementing a variable used as a counter:
a = a + 1
This remindes me of the
+1thing we used to do on calculators in elementary school.Try this a few times:
a += 1
What does this do?
Activity
- Write a function to add
+1to some variable 5 times and return the value. - Now do the same thing, but 10 times.
- Now do the same thing again, but 100 times.
First loops¶
Probably the most important things in a programming language.
If you’re going to pay attention only once this term... now’s the time.
So far, if we want Python to do the same thing over and over, we have to tell it explicitly by repeating those instructions over and over.
- There has to be a better way!

We want to automate the process of repeating things.
If I can put a block of instructions into a function and call that function...
... why can’t I put a block of instructions somewhere and say “Hey, do that block of instructions until I tell you to stop”?
The
whilestatement allows us to do exactly this.While some condition is true, keep doing the code in the indented block:
a = 1 while a < 11: print a a = a + 1
- That code will print the numbers from 1 to 10. Take a minute to note three things:
- Before the
whilestatement, we initialize the loop variablea - The
whilestatement is followed by a condition (which can be any boolean function!). If the condition isTrue, the body of the loop gets executed, otherwise it gets skipped. (don’t forget the:!) - What would happen if we didn’t have
a=a+1?
- Before the
Activity — Featuring LOOPZ
- Write a function to add
+1to some variable 5 times and return the value. - Now do the same thing, but 10 times.
- Now do the same thing again, but 100 times.
Consider this code:
def dostuff(n): answer = 1 while n > 1: answer = answer * n n = n - 1 return answer
Activity
What does the code above do? Trace through it, using pen and paper, for a few example values of n!
- The pattern
a = a + 1shows up so often that Python permits a shorthand for it:a += 1. If you like the shorthand, use it. If you don’t: don’t. It’s not mandatory; just saves some typing. whileloops can get complicated quickly. Much of the time, it is by no means obvious what they do.- If you’re faced with such a loop, trace through the execution of the loop by building a table of values.
- Let’s trace
dostuff(4). We’ll look at the values ofnandanswerright after thewhilestatement.
| n | answer |
|---|---|
| 4 | 1 |
| 3 | 4 |
| 2 | 12 |
Activity
Write a function intsum(n) that takes a single integer n as a parameter and returns the sum of all of the numbers between 1 and n.
Trace through your function for the call intsum(5)
Activity
Modify intsum(n) so that it prints out a Trace table, like the one you did by hand, every
time it runs.
Don’t worry about formatting the table, just print out the values.
Encapsulation¶
Big word for a simple idea: take your code and “encapsulate” it in a function.
That’s it.
- Normal development process for scientific software:
- Screw around at the interpreter prompt for a while
- Get something that you like
- Get tired of typing those commands over and over
- Encapsulate that set of commands in a function
- Back to messing around at the interpreter prompt, but with your new function
- Get something you like
- Get tired of typing thhose commands over and over...
- ...
OMG some actual science!¶
- Okay, maybe not. But we’re taking a step in that direction.
Activity
Find the solution to the equation:
Okay, that’s a tough one, so you get some help. How do we go about it?
Let’s use something called Newton’s Method .
Since I promised this is a no-prerequisite course, I’ll restrain myself from telling you the explanation of how the method works. I really want to, though. You only need first year calculus...
- Here’s what you do:
Pick a value
xbetween 0 and 1. Any will do. Seriously.- Compute:
The answer to that equation is an approximation of the solution
It’s not a very good approximation yet. What to do?
Set
xequal to the new approximation and plug in to the formula again.Presto! New approximation.
Still not good enough? Guess what?
Set
xequal to the new approximation and plug in to the formula again.
Stopping myself from explaining the theory behind this is excruciating. Gotta focus.
- What you want to do is:
- write a function
approx_xthat, given an approximation for x, computes the formula I gave you - write another function, that calls this function
while x != approx_x
- write a function
Algorithm¶
What you just saw, Newton’s method, is an example of an algorithm.
An algorithm is a description of a series of steps to solve a problem.
Algorithms can be presented in natural language, but are easier to turn into a program when presented in a formal language.
Finding an algorithm to solve most problems is very hard. You can make a career, get tenure, make millions of dollars in patent licensing, etc., “just” by developing algorithms.
As scientific programmers, we will usually combine existing algorithms to do what we want. We won’t often be desigining our own from scratch.
- The two most important concepts you will learn in this course (or really, what a computer scientist spends years learning) are:
- ALGORITHM
- DATA STRUCTURE
So we’re half done! (Just kidding)
Activity
Write down (in English) an algorithm for printing out the sum of all the even numbers between 1 and n.
Now convert the algorithm into a Python function.
Test it.
Numerical Methods¶
- Newton’s Method belongs to a special subclass of algorithms called Numerical Methods .
- As a scientist, you’ll come up against numerical methods a lot.
- ... especially iterated methods. Newton’s algorithm works by successively approximating an answer. It never actually finds the “one true analytical answer”, it just gets you a close enough approximation.
- That sounds messy... but the upside is that it works for problems that are completely unsolvable analytically.
- The price to pay is... vigilance. We’ll dig into details later, but keep your eyes open.
Activity
How would your approx_x function differ if x had type numpy.float32 vs numpy.float64?
Guess first, then try it and see!