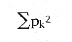

What is Biodiversity?
The term “biodiversity” is used all too frequently, by biologists
and non-biologists alike, as though it had a definite meaning. In fact, it doesn’t.
For many people the term simply means the number of species in a natural place,
but this meaning is pre-empted by the term “richness.” If one wants
to measure “biodiversity” there are no less than 12 different definitions
to choose from, all of them different. Most definitions of biodiversity involve
a formula that includes not only the number of species in a place, but the abundances
(absolute or relative) of those species, as well.
For example, the popular Simpson biodiversity index,
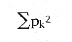
Another popular index due to Claude Shannon, the well-known information theorist at Bell Labs during the 40s and 50s, also uses relative abundances.
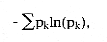
Not one proposal for a definition of biodiversity takes actual abundance distributions into account. This area of theoretical ecology is in a major (largely unrecognized) crisis, owing to a plethora of purely speculative models with little or no foundation in biological reality. Theoreticians have misled their applied colleagues who want to say something meaningful about the communities of living things which they study. The area of species-abundance distributions and biodiversity studies is riddled with guesswork and an almost complete lack of scientific discipline. None of the guesses, whether about general mechanisms, abundance distributions, or biodiversity measures, appear to have been rigorously tested or, in some cases, tested at all. All too often, writers of textbooks pass these guesses along as if they amounted to some kind of comprehensive theory, instead of the hodgepodge they are.
One of the most telling problems with the field is that no comprehensive theory relating samples of a community to the community itself exist. A field biologist who wants to estimate the abundances of a community of interest will find himself or herself almost completely without guidance on how to proceed. (Dewdney 98)
In what follows, some definitions will be necessary: First, a locale is a region of the biosphere defined in space-time by definite spatial and temporal boundaries. The supercommunity of a locale is the set of all species in it. A community is a subset of the supercommunity, usually defined (in practice) in terms of ecological niche or taxonomic group. The biodiversity vector of a community is the list of abundances of its species, taken either in canonical (taxonomic) order or in decreasing order. In the latter case, it may also be called the rank abundance vector.
The aim of biodiversity assessment of a community is nothing other than the derivation or determination of its biodiversity vector by making inferences from samples of the community. The most important unsolved problem of theoretical ecology is to discover a) whether there is a distribution that describes species abundances of communities generally and b) what general mechanism, if any, accounts for the distribution.
RESEARCH ANNOUNCEMENT July 7 2001
THE SHAPE OF ABUNDANCE: THE CENTRAL PROBLEM OF THEORETICAL ECOLOGY
An individual-based dynamical system (Dewdney 1997) models thousands of individuals belonging to hundreds of species that interchange energy/biomass, individuals dying or reproducing in consequence. The new dynamical system, called the multi-species logistic or MSL system, produces species abundance distributions that are statistically indistinguishable from distributions that biologists and ecologists have been finding in the field since the beginning of systematic sampling. (Dewdney 00)
When numbers of species are plotted against abundances in such samples, the lowest abundance category typically contains the most species. The category of next higher abundance contains distinctly fewer species, the numbers declining thereafter in the same fashion until they level off and converge to 0 at the high end of the abundance axis. Ecologists know this shape informally as the “J-curve” or, sometimes, the “hollow curve.” Several formulas have been proposed for this shape, only two enjoying current favour: the log-series and lognormal distributions. I will discuss these distributions presently.
The dynamical system mentioned above is a computer program that embodies extremely simple rules governing the trophic and reproductive behavior of as many interacting (artificial) species as the experimenter wishes to study. The system iteratively selects individuals at random, transferring a unit of biomass from one to the other. At the simplest level, the “biomass” consists of the whole individual. The one individual “dies” and is removed from the simulation, while the other individual reproduces itself. In its most general form, the transfer can be interpreted variously as predation, trophic theft (as when one plant shades another), or even as fungal or bacterial decomposition. The system seems, moreover, capable of endless complication and elaboration without failing to produce curves in the same two-parameter family (as defined below). For example, the species may be divided into trophic compartments roughly equivalent to plants, herbivorous animals, carnivorous animals, and fungi/bacteria; the logistic-J distribution results. One may substitute fractional trophism for integral trophism; the logistic-J distribution results (Dewdney 97). One may cause the probabilities of trophism/reproduction and death to fluctuate randomly about their means; the logistic-J distribution results.
At equilibrium, the dynamical system continuously produces abundances that, when plotted, reveal the typical J-curve shape. Analysis of the dynamical system in this state reveals a very simple underlying solution curve, a hyperbolic section called the logistic-J distribution: The distribution has two parameters, epsilon and delta, the sectioning constants. The probability density function (pdf) has a simple form.
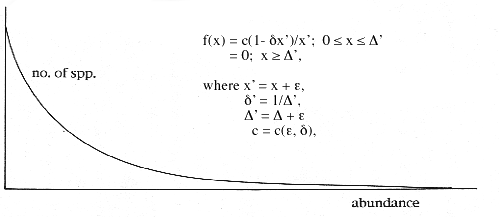
This form of the logistic-J distribution is called the general logistic-J. A very close approximation, which can be used in the field, is called the special logistic-J. It has the same hyperbolic form, but employs the parameter epsilon in a mathematically simpler way that, while not entirely suitable for the description of abundances in communities, works just as well as the general logistic-J on samples of those communities.
The special logistic-J is defined as follows:
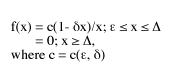
For the last five years, I’ve been engaged in a massive study of the logistic-J distribution, comparing its predictions with the distributions that arose in 125 biosurveys conducted by as many experienced and reputable field biologists. See the bibliography.
The metastudy
One hundred and twenty-five biosurveys were randomly selected and compared, via the chi-squared test, with the special logistic-J distribution, the general logistic-J distribution, and with the log-series distribution, easily the closest competitor with the logistic-J distribution (either version) as the descriptor of choice for natural species abundance distributions.
The biosurveys were taken in every major type of habitat, from ocean benthos to mountain rain forest. They span all climates, from polar to tropical. They include five kingdoms and, within most of those kingdoms, dozens of phyla, classes and orders. The groups studied in these biosurveys include: Cyanobacteria, zygomycetes, ciliates, siphonaptera, orthoptera, coleoptera, arachnida, lepidoptera, aves, pisces, mammalia, lichens, bryophytes, angiosperms (herbaceous and woody), among others. The selection process involved 1. the random selection of a biosurvey, then 2. the application of a simple filter to rule out unsuitable studies. The filter rejected surveys with fewer than 30 species or surveys that provided only order-of-magnitude abundance data, or surveys that omitted species with low abundances. See the test data.
A metastudy is unavoidable for anyone wishing to investigate the presence of any theoretical distribution of abundances in nature. Owing to a general and deep misunderstanding of statistical testing among theoretical ecologists, it has apparently been thought sufficient to compare a given theoretical proposal with a mere handful of distributions, noting a purely visual resemblance and not even bothering with a goodness-of-fit test!
Anyone wishing to conduct such an investigation, must first attempt to reject their proposal by employing a recognized goodness-of-fit test to compare their proposal with abundance data from the field. Failure to reject the theoretical distribution, however, does not mean it is correct. It is somewhat disappointing to realize that theoretical ecologists have not understood that any theoretical proposal with approximately the right shape (and there is an infinite number of these, all different) is likely to be “accepted” by a goodness-of-fit test.
The only recourse of the investigator who cannot consistently reject a theoretical proposal is to carry out this comparison with a great many field distributions, at least 100 for starters. This conclusion is based solidly on the foundations of statistical theory and is unavoidable. (Any biologist/ecologist who uses statistical tests of any kind is relying on the same general foundations of hypothesis-testing.)
The statistical test employed for this metastudy was the chi square distribution, employed in the standard way, to obtain a score for each of the special and general logistic-J, as well as for the log-series distribution. To make the scores obtained at different degrees of freedom comparable, they were converted to an equivalent score at ten degrees of freedom. If the null hypothesis is correct (all natural abundance distributions differ from the logistic-J only by chance) one would expect an average score of approximately 10 as “ideal.” The chi square distribution has a relatively high variance, however, so any average score within one unit of 10 would be extremely hard to rule out. See test scores.
The scores achieved by the three distributions are listed below:
| Distribution | Mean | Standard Deviation |
| Special Logistic-J | 10.84 | 5.33 |
| General Logistic-J | 10.81 | 5.51 |
| Log-series | 13.56 | 9.40 |
Another, more telling use of the converted chi square scores made it possible to reject the log-series distribution as a general candidate descriptor of natural abundance distributions. A paired difference test revealed a significant gap between the (special) logistic-J distribution and the log-series distribution. In this test, the differences between the former and latter distributions were computed for each biosurvey, producing the same effect as controlling for all variables except the scores of the respective distributions on it. This test produced the following confidence interval for the mean difference of 2.658 between scores for the special logistic-J and the log-series distribution over all 125 biosurveys:
[1.325, 3.991] (t-value 0.025)
The fact that the interval is bounded away from 0 means that with probability of only 0.025 we would err in asserting that the population of test scores for the log-series distribution is different from that of the logistic-J distribution. In other words, there is a statistically discernible difference between the two populations, as revealed by their test scores. Since the logistic-J distribution scored lower (i.e., better) on the 125 biosurveys, we may assert that it is, with very high probability (0.975) the superior descriptor of community abundances in the most general sense.
We can do even better than this. The average difference of 2.658 in test scores is bounded away from 0 by an even larger interval that corresponds to an even smaller t-value:
[0.578, 4.738] (t-value 0.001)
In short, it may be claimed that the special logistic-J distribution outperforms the log-series distribution by a statistically discernible margin over all possible field biosurveys (of the type with which we are familiar, at least) with a probability of 0.999. The same thing is true for the general logistic-J, as well. It also comes in with a slightly lower average score than the special distribution, although this is quite possibly accidental.
A third finding also supports the reality of the logistic-J distribution. The distribution predicts a specific value DELTA’ for the average maximum population in a community. When one forms the ratio of the maximum population in a given biosurvey with the theoretical prediction, DELTA, one obtains, typically, a number DELTA’/DELTA somewhere between 0.3 and 1.5. The average such ratio, taken over all 125 biosurveys, is shown for both versions of the logistic-J distribution in the next table:
| Distributions | average ratio (%) of actual to theoretical maximum abundance |
| Special logistic-J | 100.4 |
| General logistic-J | 107.8 |
What makes this finding remarkable is that it is even approximately correct. What are the chances that a randomly chosen finite distribution would predict a limit which, on average, was accurate to within one order of magnitude (a factor of 10)? Very small indeed.
Nothing like this amount of evidence has ever been produced in favor of a theoretical proposal for species abundances in nature. Unfortunately, that is nothing to brag about!
In any case, the log-series distribution has been rejected overwhelmingly as the theoretical distribution of choice. Of all extant proposals, it was certainly the closest in shape to the logistic-J distribution.
The lognormal distribution
Another very popular candidate for species/abundance distribution is the lognormal. A fatal mathematical error has been found at the theoretical foundation of the lognormal distribution; the so-called “veil line” is a mathematical fiction. (Dewdney 98). The species in a community that will go missing from a sample of that community is not represented by an arbitrary vertical truncation, but a curving, sigmoidal section. The removal of this section from the (untruncated) lognormal simply results in a new lognormal curve that remains untruncated, in effect. There is simply no hope that this distribution will fit empirical data. Nothing like it was found in any of the 125 biosurveys admitted to the study.
Moreover, when the logistic-J distribution is treated to a logarithmic transformation of the sort performed for the lognormal (i.e., division of the abundance categories into octaves), the resulting curve looks surprisingly like a (vertically) truncated normal distribution. But it isn’t. This curve results from a roughly linear buildup of species in the initial octaves, gradually but increasingly diminished by an exponentially growing subtractive term. The resulting distributions would readily pass goodness-of-fit tests against the (truncated) normal distribution. If natural communities are logistic-J distributed, this would explain why the (truncated) lognormal sometimes appears to fit.
The stochastic hypothesis
Analysis of the dynamical system reveals two very simple mechanisms at work, mechanisms that are even more fundamental than trophism per se. In the first mechanism, an individual has an even chance of increasing (reproducing) on average, as it does of decreasing (dying). The second mechanism is conservation of biomass (or energy) as the system runs. The second mechanism is crucial and to signal this, the word "logistic" appears in the name of the resulting distribution.
We call the tendency for birth and death probabilities to be equal the stochastic species hypothesis. It is a highly remarkable and hitherto unknown fact that any system (natural or artificial) that obeys this hypothesis, does not lead to what ecologists call “equilibrium” or “regulated” populations in a community. A large number of populations will drift toward low abundance, while a few populations will drift, with equal certainty, to very high abundances. As the system progresses, some of the low abundance populations become numerous again while one or more of the high-abundance populations will decline in numbers. All of this happens without the probabilities ever failing to be equal! This result, which has been verified too often to be wrong, a result which has also been established mathematically, constitutes the core insight of the stochastic species hypothesis. It is counter-intuitive, to say the least.
The stochastic species hypothesis is certainly true in the long run for all species. Suppose, for example, that a population of N individuals belonging to a certain species has n births and m deaths over one reproductive cycle. The ratios n/N and m/N form two unbiased estimates of the probability of birth and death respectively over the period in question. The ratio of these estimates is simply n/m and the long term behaviour of this ratio is readily examined. If there are ni births and mi deaths during the ith reproductive cycle the ratio will become, after k cycles,
If the species in question has an average life span of r cycles, we may make k arbitrarily large in relation to r and observe that the first M births result in the same number of deaths, so that
as M increases. In the limit, of course, R = 1.
It is even posible to allow the probabilities themselves to fluctuate up and
down within the system. As long as they hover about equality, they will produce
the behaviour we observe.
Stochasticity in species abundance has been suspected for a long time by many ecologists. Simply put, the many, many factors affecting abundance do not always work harmoniously with each other. This produces, in consequence, motions along the abundance axis that could be termed “effectively random.” The stock market is explicable as the rational outcome of thousands of investment decisions, but the resulting patterns of buying and selling are “effectively random,” with fluctuations over all temporal scales.
At first sight, this hypothesis would appear to excuse a great throwing up of the hands. Instead, it poses a challenge. Mechanisms such as exclusion, succession, competition, etc. are undoubtedly present in nature, but these and many other factors depend directly or indirectly on many other factors including that major determinant, weather. The latter is well known to be effectively random, being subject to the sensitivity to initial conditions that we call “chaos.” The stochastic species hypothesis provides a comprehensive conceptual framework within which various mechanism may be investigated.
Biodiversity and evolution
Theoretical ecology has provided little or no leadership to field biologists and ecologist who seek to describe and understand natural communities of living organisms. Many of the papers surveyed in the metastudy dutifully calculate various indices of “biodiversity,” but say little about the significance of these measures. This is due to the fact that, in essence, they have none.
Secondly, it is unclear how a single number is supposed to express both species richness and the range of abundances that those species have. With an agreed-upon model of abundances, such as the stochastic model and its accompanying logistic-J distribution, a real start can be made at putting the study of natural communities on a sound footing. The two distribution parameters (epsilon, the average minimum abundance, and delta, the average maximum abundance) serve to specify a logistic-J curve completely and thus to describe an entire community to within normal statistical fluctuations. Other, equivalent two-parameter choices would include maximum abundance and average abundance.
In some ways the most exciting implication of the new theory is the assertion that not only are species “vibrating stochastically,” but genera are, as well. When extinction and speciation are considered in place of death and reproduction, the hypothesis (with all of its logical consequences) provides a rather pretty explanation for an old puzzle: when you plot the number of genera of birds (or any other well-known taxonomic group) per numbers of species, you get a J-curve, one that fits the logistic-J distribution rather well on average. And what is true for species within genera is also true for genera within families, and so on. These are, in effect, “fossil J-curves.”
The implications of the stochastic species hypothesis for evolution are profound. For one thing, an outstanding puzzle of the modern theory of evolution, the “cohesive gene pool effect,” is solved. The number of small, isolated populations, in all groups of organisms, is far larger than theorists had hitherto realized. Here is a mechanism by which new genes (resulting from mutation within a small population) take hold. Since such populations frequently regain their former numbers, they bring with them the new gene and introduce it (if not reproductively isolated) to the metapopulation of which they form a part.
Listed below are four papers that represent the published output relating to the dynamic model, the logistic-J distribution, and the stochastic hypothesis at this time. More publications are one the way. If you would like to be on a mailing list for subsequent papers (including a field manual for biologists, ecologists, geographers, etc.) don’t hesitate to email the author: <akd@uwo.ca>
A. K. Dewdney
Dept. of Zoology
(& Dept. of Computer Science)
University of Western Ontario
London, Ontario N6A 5B7 (519) 661-3557 or 679-8105
Dewdney, A. K. 1997. A dynamical model of abundance in natural communities. COENOSES 12 (2&3): 67-76
Dewdney, A. K. 1998. A general theory of the sampling process with applications to the “veil line.” Theor. Pop. Biol. 54(3): 294-302.
Dewdney, A. K. 2000. A dynamical model of communities and a new species-abundance distribution. The Biol. Bull. 198(1): 152-163.
Dewdney, A. K. 2001. The forest and the trees: romancing the J-curve. The Mathematical Intelligencer 23(3): 27-43.
There are more papers to follow. A monograph is also currently in preparation copies of which may be ordered from the author by active researchers.
The Multi-species Logistical System
Let an (abstract) community C consist of N individuals distributed among m species. The computer model described here is dynamical, stochastic and individual-based. The basic dynamical step selects two individuals at random (the stochastic element) from the general population of N individuals. The basic system appears to be “detail hungry”, meaning that it seems capable of unlimited complication whilst preserving the shape of abundance histograms that it produces, Versions of the program involving fractional trophism, abstract food webs, “real” food webs (with standard trophic compartments) have all been written and successfully tested.
To guarantee randomness at the individual level, selections are made on a proportional basis by the interval division technique: A procedure invoked by the main program selects a random number between 1 and N, then counts through the species by their abundances until it comes to the species where the count first equals the randomly drawn number. In the algorithmic conventions employed here, variable names are set in italics, the assignment operator is indicated by a left-arrow, and pseudo-language elements are set in bold face:
procedure Select Species
select a random number k from [1, N]
Count <-- 0, s <-- 0
repeat
Count <-- Count + abundance of s
s <-- s + 1
until count >= k
return s
The basic algorithm for the dynamical system is extremely simple. Within a user-terminated loop, the procedure just defined makes a random selection of two individuals, returns their species id numbers, and then alters their abundances according to the following scheme.
repeatPredator <-- Select Species
Prey <-- Select Species
increment abundance of Predator
decrement abundance of Prey
until key pressed
Abundances of the m species are stored in an array called Abundance.
You may view this algorithm in action by clicking the button below. You will be asked to select a number of species and an initial abundance for all species. Admittedly, no natural community of organisms ever has a uniform abundance, but it is a programming convenience to initialize the system with all species at the same abundance. However, no matter what distribution one starts with, the system always moves toward the logistic-J distribution, a phenomenon you will witness here. The larger you choose the initial population size to be, the longer it will take the system to reach equilibrium.
It should be remarked that more general programs that follow the stochastic species hypothesis more directly show precisely the same behavior.
Anyone with programming experience should be capable of writing a program based on this algorithmic description. The program was written by the author in Turbo Pascal. It runs on a 486 computer and incorporates the basic algorithm within a display loop of 100 iterations. It also includes a histogram-drawing procedure that uses text graphics to show the number of species at each abundance value. Again, it must be stressed that although this system is labelled here as though it were a predator/prey system, it is in fact far more general. The more elaborate models (that produce exactly the same distribution) are simply about the transfer of energy, everything from photons to prey biomass.
For those without programming skills but the talent to enter a program via keyboard, here is the Turbo Pascal version of the algorithm given above.
PROGRAM Scramble1.1
{Scramble1.1 simulates a community of organisms}
{interacting under the constant energy/biomass rule.}
USES Crt;
VAR Pred, Prey, I, J, K, Cat, Ext, NumSpec: INTEGER;
VAR Ticks, Cycles, Total, Pop, MaxAbund: INTEGER;
VAR MaxSum LONGINT;
VAR Choice, AvHist, AvMax: REAL;
VAR Click: BOOLEAN;
VAR Extinctions: CHAR;
{Constant Declarations: Set remaining options by changing appropriate}
{constants declared below. Note that Range = 1 may cause screen buffer}
{overwrite if Pop is very large.}
CONST Range = 3; {size of abundance categories in report}
CONST Start = 2000; {MSL in equilibrium by this many cycles.}
CONST Stop = 2500; {End run by this many cycles.}
{Array declarations: Abunda holds abundances of species, while Hist}
{holds species/abundance histogram.}
TYPE BioArray = ARRAY[1 . . 300] OF INTEGER; {edit if # spp.. > 300}
VAR AbundA: BioArray;
TYPE BioStats = ARRAY[0 . . 150] OF LONGINT; {edit for > 150 categories}
VAR Hist, HistSum: BioStats;
{The following procedure selects a random individual -- not species.}
PROCEDURE Selector(PPop: INTEGER; PrArray: BioArray; VAR Choice: INTEGER);
VAR Select: INTEGER;
VAR Count, Interval, Total: INTEGER;
BEGIN
Total := 0;
Select := RANDOM(NumSpec*PPop) + 1;
Count := 0; Interval := 0;
{Interval division loop}
WHILE Interval < Select DO
BEGIN
Count := Count + 1;
Interval := Interval + PrArray[Count];
END;
Choice := Count;
END;
BEGIN {main program}
{Interface section}
WRITELN(¡®Scram1.1 Community Simulator: system options not appearing¡¯);
WRITELN(¡®here can be specified by editing the program declarations.¡¯);
WRITE(¡®Enter the number of species in the community: ¡®);
READLN(NumSpec);
WRITE(¡®Enter initial population sizes: ¡®);
READLN(Pop);
WRITE(¡®Do you want extinctions? (y or n): ¡®);
READLN(Extinctions);
{initializing section}
RANDOMIZE;
CLRSCR;
Click := FALSE;
Cycles := 0;
Ticks := 0;
MaxSum := 0;
{clear histogram}
FOR J := 1 TO 66 DO
BEGIN
HistSum[J] := 0;
Hist[J] := 0;
END;
{set up initial populations}
FOR I := 1 TO NumSpec DO
AbundA[I] := Pop;
{main loop}
WHILE (NOT KEYPRESSED) AND (Cycles < Stop) DO
BEGIN
FOR J := 1 TO 100 DO {100 iterations per cycle}
BEGIN
{Select a ¡°predator¡± (individual).}
Selector(Pop, AbundA, Pred);
{Select a ¡°prey¡± (individual).}
Selector(Pop, AbundA, Prey);
IF ((Extinctions = ¡®y¡¯) AND Click) OR (AbundA[Prey] > 1)
THEN BEGIN
AbundA[Prey] := AbundA[Prey] - 1;
AbundA[Pred] := AbundA[Pred] + 1;
END;
END;
{Build the histogram.}
Ext := 0;
MaxAbund := 0;
FOR J := 1 TO NumSpec DO
IF AbundA[J] = 0
THEN Ext := Ext + 1;
ELSE BEGIN
Cat := TRUNC((AbundA[J]-1)/Range) + 1;
Hist[Cat] := Hist[Cat] + 1;
IF AbundA[J] > MaxAbund THEN MaxAbund := AbundA[J];
END;
{Display the histogram.}
CLRSCR;
GOTOXY(1, 1,);
FOR J := 1 TO 24 DO
BEGIN
IF Hist[J] >= 1
THEN FOR K := 1 To Hist[J] DO
WRITE(¡®*¡¯);
WRITELN;
END;
{Add the histogram to the average.}
IF Cycles > Start THEN Click := TRUE;
IF Click THEN
BEGIN
FOR J := 1 TO 150 DO
HistSum[J] := HistSum[J] + Hist[J]
Ticks := Ticks + 1;
MaxSum := MaxSum + MaxAbund;
END;
{Clean the histogram.}
FOR J := 1 TO 150 DO
Hist[J] := 0;
{Report parameters.}
Cycles := Cycles + 1;
GOTOXY(50, 15);
WRITELN(¡®extinct: ¡®, Ext);
GOTOXY(50, 16);
WRITELN(¡®Cycles: ¡®, Cycles);
GOTOXY(50, 17);
WRITELN(¡®# spp.. & mean: ¡®, NumSpec, ¡® & ¡®, Pop);
GOTOXY(50, 18);
WRITELN(¡®max abundance: ¡®, MaxAbund);
GOTOXY(50, 19);
WRITELN(¡®start & stop: ¡¯, Start, ¡® & ¡®, Stop);
END; {of main loop}
{Report average histogram values.}
FOR J := 1 TO 150 DO
BEGIN
AvHist := HistSum[J]/Ticks;
WRITE(AvHist:5:2, ¡® ¡®);
IF J MOD 10 = 0 THEN WRITELN
END;
AvMax := MaxSum/Ticks;
WRITELN;
WRITELN(¡®average maximum: ¡®, AvMax:7:2);
READLN {to preserve user screen}
END. (of program}
Note: Before running the program, experimenters may alter some of the internal constants by simply editing the three CONST statements.
Return to A.K. Dewdney's Home Page