
A hypothetical sample of freshwater fishes
The Shape of Biodiversity
Recent research & publications
A.K. Dewdney
Since 1995 I have been pursuing the following important question: “Do the abundances of species in a community follow a single, universal distribution or several different ones, depending on the community?”

A hypothetical sample of freshwater fishes
The usual way to assess the abudances (population sizes) of species in a community of organisms is to sample it, counting the number of individuals in each species that appears in the sample. One may then plot the number of species with each possible abundance: 1, 2, 3, and so on. It is an observation of the highest significance that no matter what sort of community is sampled, the same basic shape shows up. This can be seen in the figure below, where some 15 different sample plots are shown. That shape is sometimes called the “hollow curve” or the “J-curve”, owing to its resemblance to the letter J lying on its side.
Since the late 1930s, theoretical ecologists have been seeking ways to infer the corresponding abundances in the community from which the sample was drawn. After all, in most applications, the community is the natural focus of interest. What is the “shape” of its abundance, so to speak. Does that shape resemble the shape of the sample? There have been many proposals for this shape and most theorists still believe that each has a role to play. The research reported here strongly implies that there are not many shapes, but just one.
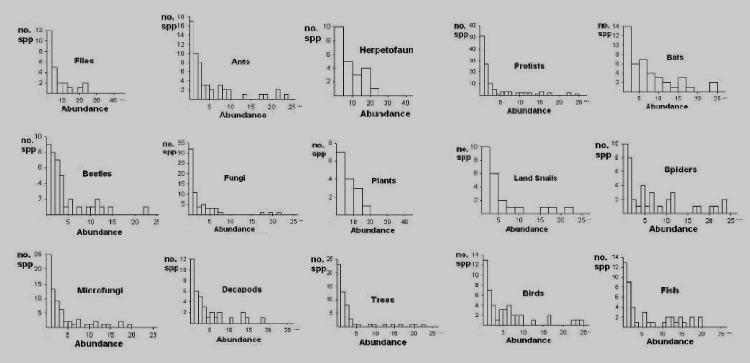
Sample J-Curves for some different organisms
My research over the past 17 years has consisted mainly in exploring the role of a specific theoretical shape called the logistic-J distribution in both real and abstract communities. This work may be divided into the following areas:
metastudy: some 125 biosurveys were selected at random from the literature and subjected to an extensive set of statistical tests that compared the biosurvey samples to two theoretical distributions. (See map at bottom of this page for sample sites.) sampling theory: this work culminated in a theorem: a sample tends to follow the same distribution that governs the community from which it was drawn, except for a change in parameter values. dynamical systems: a simple individual-based process that implies the long-term equality of birth and death probabilities produces the logistic-J distribution. The process is detail-hungry, with many forms. |
The following results have been obtained during this research:
The metastudy revealed that the logistic-J distribution achieved a near- optimal overall score, outperforming its closest competitor, the log-series distribution, by a statistically significant margin.
The general sampling theorem has many implications, including the conclusion that there is no “veil line” that masks low-abundance species in samples. Low abundance species show up with the expected frequency.
The equality of birth and death probabilities, called the stochastic species hypothesis, may be deployed in a huge variety of models, from those employing strict equality to those employing a varying, long-term equality. Also included are models with trophic compartments that mimic real food webs, to models in which the communities themselves are divided into compartments with specifiable migration rates between them.
My contributions to the literature have been relatively modest owing largely to the enormous speed with which the theory has developed. The following publications include my main contributions to the field of theoretical ecology:
1997. A dynamical model of abundance in natural communities. COENOSES 12 (2&3): 67-76. 1998. A general theory of the sampling process with applications to the "veil line." Theor. Pop. Biol. 54: 294-302. 1998. A dynamical model of communities and a new species-abundance distribution. Biological Bulletin 198: 152-165. 2001. The forest and the trees: romancing the J-curve. Math. Intelligencer 23 (3): 27 - 34. 2003. The stochastic community and the logistic-J distribution. Acta Oecologica 24: 221-229. 2008. Cellular Automata. pp 541-550 in The Encyclopedia of Ecology (S. E. Jorgensen & Brian Fath, eds.) Elsevier, Oxford. 2010. The Structure and Distribution of Benthic Microbial Communities in the Old Ausable River Channel. (in) Response of an Aquatic Ecosystem to Human Perturbation: Hydroecology and Geochemistry of the Old Ausable Rive Channel. (M. A. Maun, ed.) National Research Council, NRC Books. Ottawa, Ontario. Rather than write an endless series of articles, it seemed more efficient to put the entire theory into a single book. Nevertheless, I have just begun to write a new series of journal articles that "catch up" to the main developments described in the monograph (now in its third draft). |
A global map of the sampling sites that provided data for the metastudy that
establishes the universal presence of the J distribution in living communities.
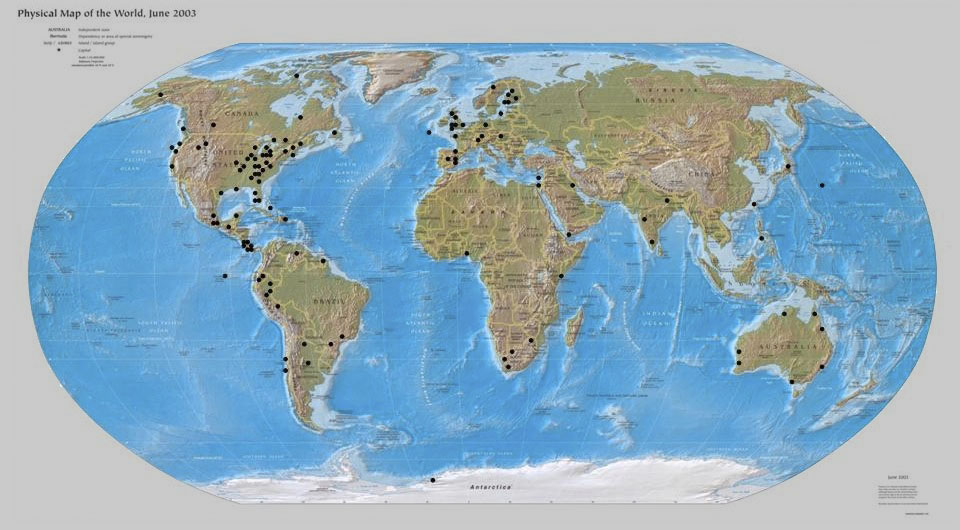 Global Map of Metastudy Biosurvey Sites |
||