A linear boundary might be too simple to capture the class structure.
One way of getting a nonlinear decision boundary in the input space is to find a linear decision boundary in an expanded space (similar to polynomial regression.)
Thus, \({{{\mathbf{x}}_i}}\) is replaced by \(\phi({{{\mathbf{x}}_i}})\), where \(\phi\) is called a feature mapping
2017-10-24
Nonlinearly separable data
Separability by adding features
Separability by adding features
Separability by adding features
more flexible decision boundary \(\approx\) enriched feature space
Margin optimization in feature space
- Replacing \({{{\mathbf{x}}_i}}\) with \(\phi({{{\mathbf{x}}_i}})\), the dual form becomes:
| max | \(\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i,j=1}^n{{y}}_i{{y}}_j\alpha_i\alpha_j({\phi({{{\mathbf{x}}_i}})\cdot\phi({{{\mathbf{x}}_j}})})\) |
| w.r.t. | \(\alpha_i\) |
| s.t. | \(0\leq\alpha_i\leq C\) and \(\sum_{i=1}^n\alpha_i{{y}}_i=0\) |
Classification of an input \({\mathbf{x}}\) is given by: \[h_{{{\mathbf{w}}},w_0}({{{\mathbf{x}}}}) = \mbox{sign}\left(\sum_{i=1}^n\alpha_i{{y}}_i({\phi({{{\mathbf{x}}_i}})\cdot\phi({{{\mathbf{x}}}})})+w_0\right)\]
Note that in the dual form, to do both SVM training and prediction, we only ever need to compute dot-products of feature vectors.
Kernel functions
Whenever a learning algorithm (such as SVMs) can be written in terms of dot-products, it can be generalized to kernels.
A kernel is any function \(K:\mathbb{R}^n\times\mathbb{R}^n\mapsto\mathbb{R}\) which corresponds to a dot product for some feature mapping \(\phi\): \[K({{{\mathbf{x}}}}_1,{{{\mathbf{x}}}}_2)=\phi({{{\mathbf{x}}}}_1)\cdot\phi({{{\mathbf{x}}}}_2) \text{ for some }\phi.\]
Conversely, by choosing feature mapping \(\phi\), we implicitly choose a kernel function
Recall that \(\phi({{{\mathbf{x}}}}_1)\cdot \phi({{{\mathbf{x}}}}_2) \propto \cos \angle(\phi({{{\mathbf{x}}}}_1),\phi({{{\mathbf{x}}}}_2))\) where \(\angle\) denotes the angle between the vectors, so a kernel function can be thought of as a notion of similarity.
Example: Quadratic kernel
Let \(K({\mathbf{x}},{\bf z} )= \left({\mathbf{x}}\cdot {\bf z}\right)^2\).
Is this a kernel? \[K({\mathbf{x}},{\bf z}) = \left( \sum_{i=1}^p x_i z_i\right) \left( \sum_{j=1}^p x_j z_j \right) = \sum_{i,j\in\{1\ldots p\}} \left( x_i x_j \right) \left( z_i z_j \right)\]
Hence, it is a kernel, with feature mapping: \[\phi({\mathbf{x}}) = \langle x_1^2, ~x_1x_2, ~\ldots, ~x_1x_p, ~x_2x_1, ~x_2^2, ~\ldots, ~x_p^2 \rangle\] Feature vector includes all squares of elements and all cross terms.
Note that computing \(\phi\) takes \(O(p^2)\) but computing \(K\) takes only \(O(p)\)!
Polynomial kernels
More generally, \(K({\mathbf{x}},{{\mathbf{z}}}) = (1 + {\mathbf{x}}\cdot{{\mathbf{z}}})^d\) is a kernel, for any positive integer \(d\).
If we expanded the product above, we get terms for all degrees up to and including \(d\) (in \(x_i\) and \(z_i\)).
If we use the primal form of the SVM, each of these will have a weight associated with it!
Curse of dimensionality: it is very expensive both to optimize and to predict with an SVM in primal form with many features.
The "kernel trick"
If we work with the dual, we do not actually have to ever compute the features using \(\phi\). We just have to compute the similarity \(K\).
That is, we can solve the dual for the \(\alpha_i\):
max \(\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i,j=1}^n{{y}}_i{{y}}_j\alpha_i\alpha_j K({\mathbf{x}}_i,{\mathbf{x}}_j)\) w.r.t. \(\alpha_i\) s.t. \(0\leq\alpha_i\leq C\), \(\sum_{i=1}^n\alpha_i{{y}}_i=0\) The class of a new input \({\mathbf{x}}\) is computed as: \[\hspace{-0.5in}h_{{{\mathbf{w}}},w_0}({\mathbf{x}}) = \mbox{sign} \left( \sum_{i=1}^n \alpha_i y_i K({\mathbf{x}}_i,{\mathbf{x}}) + w_0 \right)\]
Often, \(K(\cdot,\cdot)\) can be evaluated in \(O(p)\) time—a big savings!
Some other (fairly generic) kernel functions
\(K({\mathbf{x}},{{\mathbf{z}}})=(1+{\mathbf{x}}\cdot{{\mathbf{z}}})^d\) – feature expansion has all monomial terms of degree \(\leq d\).
Radial basis/Gaussian kernel (most popular): \[K({\mathbf{x}},{{\mathbf{z}}}) = \exp(-\|{\mathbf{x}}-{{\mathbf{z}}}\|^2/2\sigma^2)\] The kernel has an infinite-dimensional feature expansion, but dot-products can still be computed in \(O(n)\)!
Sigmoid kernel: \[K({\mathbf{x}},{{\mathbf{z}}}) = \tanh (c_1 {\mathbf{x}}\cdot{{\mathbf{z}}}+ c_2)\]
Example: Gaussian kernel
Kernels beyond SVMs
Remember, a kernel is a special kind of similarity measure
A lot of research has to do with defining new kernel functions, suitable to particular tasks / kinds of input objects
Many kernels are available:
Information diffusion kernels (Lafferty and Lebanon, 2002)
Diffusion kernels on graphs (Kondor and Jebara 2003)
String kernels for text classification (Lodhi et al, 2002)
String kernels for protein classification (e.g., Leslie et al, 2002)
… and others!
Example: String kernels
Example: in DNA matching, we can use a sliding window of length \(k\) over the two strings that we want to compare
The window is of a given size, and inside we can do various things:
- Count exact matches, Weigh mismatches based on how bad they are, …
The kernel is the sum of these similarities over the two sequences
How do we prove this is a kernel? http://www.kernel-methods.net/
Many other machine learning algorithms have a "dual formulation," in which dot-products of features can be replaced with kernels.
Second brush with “feature construction”
With polynomial regression, we saw how to construct features to increase the size of the hypothesis space
This gave more flexible regression functions
Kernels offer a similar function with SVMs: More flexible decision boundaries
Often not clear what kernel is appropriate for the data at hand.
Getting SVMs to work in practice
libsvmandliblinearare popularScaling the inputs (\({\mathbf{x}}_i\)) is very important. (E.g. make all mean zero variance 1.)
Two important choices:
Kernel (and kernel parameters, e.g. \(\gamma\) for the RBF kernel)
Regularization parameter \(C\)
The parameters may interact!
Together, these control overfitting: always do a within-fold parameter search, using a validation set!
Clues you might be overfitting: Low margin (large weights), Large fraction of instances are support vectors
Artificial Neural Networks (HTF Ch. 11)
- Functional form + Training algorithm
Functional Form - Neuron
\(\color{red}{h^{(1)}_{1}}(\color{blue}{x_1}, \color{blue}{x_2}, \color{blue}{x_3}) = \phi^{(1)}_{1}(w^{(1)}_{1,1}\color{blue}{x_1} + w^{(1)}_{2,1}\color{blue}{x_2}, + w^{(1)}_{3,1}\color{blue}{x_3} + w^{(1)}_{0,1})\)
Functional Form
\(\color{red}{h^{(1)}_{1}}(\color{blue}{x_1}, \color{blue}{x_2}, \color{blue}{x_3}) = \phi^{(1)}_{1}(w^{(1)}_{1,1}\color{blue}{x_1} + w^{(1)}_{2,1}\color{blue}{x_2}, + w^{(1)}_{3,1}\color{blue}{x_3} + w^{(1)}_{0,1})\) \(\color{red}{h^{(1)}_{2}}(\color{blue}{x_1}, \color{blue}{x_2}, \color{blue}{x_3}) = \phi^{(1)}_{2}(w^{(1)}_{1,2}\color{blue}{x_1} + w^{(1)}_{2,2}\color{blue}{x_2}, + w^{(1)}_{3,2}\color{blue}{x_3} + w^{(1)}_{0,2})\) \(\color{red}{h^{(1)}_{3}}(\color{blue}{x_1}, \color{blue}{x_2}, \color{blue}{x_3}) = \phi^{(1)}_{3}(w^{(1)}_{1,3}\color{blue}{x_1} + w^{(1)}_{2,3}\color{blue}{x_2}, + w^{(1)}_{3,3}\color{blue}{x_3} + w^{(1)}_{0,3})\)
\(\color{purple}{h^{(2)}_{1}}(\color{blue}{x_1}, \color{blue}{x_2}, \color{blue}{x_3}) = \phi^{(2)}_{1}(w^{(2)}_{1,1}\color{red}{h^{(1)}_{1}} + w^{(2)}_{2,1}\color{red}{h^{(1)}_{2}}, + w^{(2)}_{3,1}\color{red}{h^{(1)}_{3}} + w^{(2)}_{0,1})\) \(\color{purple}{h^{(2)}_{2}}(\color{blue}{x_1}, \color{blue}{x_2}, \color{blue}{x_3}) = \phi^{(2)}_{2}(w^{(2)}_{1,2}\color{red}{h^{(1)}_{1}} + w^{(2)}_{2,2}\color{red}{h^{(1)}_{2}}, + w^{(2)}_{3,2}\color{red}{h^{(1)}_{3}} + w^{(2)}_{0,2})\)
"Activation" or "Transfer" Function \(\phi\)
| Name | Plot | Equation |
|---|---|---|
| Identity |

|
|
| Binary step |

|
|
| Logistic |
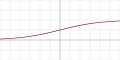
|
|
| TanH |

|
Rectified linear unit (ReLU)[9] |
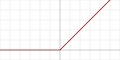
|
Hidden Units are Constructed Features
Aside: "One-Hot" Encoding
Error Functions
\[\begin{aligned} J({\bf w}) & = \frac{1}{2}\sum_{j} \sum_{i=1}^n (h^{(L)}_j({\bf x}_i)-y_i)^2\\ J({\bf w}) & = -\sum_{j}\sum_{i=1}^n y_i \log h^{(L)}_j({\mathbf{x}}_i) + (1-y_i) \log (1-h^{(L)}_j({\mathbf{x}}_i)) \end{aligned}\]
Training
Traditional ANN training is done by looping over examples (much like the perceptron) and taking a small step down the single-example gradient.
For a single output neuron:
\[\begin{aligned} J_j({\mathbf{w}}) & = \frac{1}{2} (h^{(L)}_j({\bf x}_i)-y_i)^2\\ \nabla_{\mathbf{w}}J & = (h^{(L)}_j({\bf x}_i)-y_i)\nabla_{\mathbf{w}}h^{(L)}_j({\bf x}_i)\\ & = (\phi^{(L)}_j({\bf x}_i^{\mathsf{T}}{\bf w})-y_i)\cdot \phi'^{(L)}_j({\bf x}_i^{\mathsf{T}}{\bf w}) \cdot {\mathbf{x}_i} \end{aligned}\]
Learning rule:
\[ \textbf{w}^{t+1} \leftarrow \textbf{w}^{t} - \alpha\cdot (\phi^{(L)}_j({\bf x}_i^{\mathsf{T}}{\bf w})-y_i)\cdot \phi'^{(L)}_j({\bf x}_i^{\mathsf{T}}{\bf w}) \cdot {\mathbf{x}_i}\]
where \(\alpha\) is a learning rate.
Backpropagation
\[ \textbf{w}^{(\ell),t+1}_{\cdot,j} \leftarrow \textbf{w}^{(\ell),t}_{\cdot,j} - \alpha\cdot \delta^{(\ell)}_{j}\cdot \phi'^{(\ell)}_j({\bf x}_i^{\mathsf{T}}{\bf w}^{(\ell),t}_{\cdot,j})\cdot {\mathbf{x}_i}\]
where
\[\delta^{(\ell)}_j = \left\{ \begin{array}{ll} (\phi({\bf x}_i^{\mathsf{T}}{\bf w})-y_i) & \mbox{if $(\ell)$ is the output layer} \\ \sum_k w^{(\ell)}_{j,k} \delta^{(\ell+1)}_k & \mbox{otherwise} \end{array} \right.\]
Variants of Backpropagation
Adaptive learning rate
"Momentum" or "inertia" - if weights keep changing in the same direction, change them faster.
Neural Net Design Decisions
- How many layers?
- How many nodes in each layer?
- What should \(\phi\) be?
- What should the cost function be?
- What version of backprop should I use?
- What should my learning rates be?
Derivatives of \(\phi\)
| Name | Plot | Derivative (with respect to x) |
|---|---|---|
| Identity |

|
|
| Binary step |

|
|
| Logistic |

|
|
| TanH |

|
|
| Rectified linear unit (ReLU)[9] |

|
Backprop "Conventional Wisdom"
- Small derivatives -> weights go nowhere
- In very deep networks, error gets "diluted" -> weights go nowhere
- Gets trapped in local optima
Deep Learning: "Unconventional Wisdom"
- Many layers (e.g. 10-20)
- Billions of connections
- Hundreds of millions of weights
http://www.nature.com/nature/journal/v521/n7553/full/nature14539.html
What changed?
Data explosion (Google and others)
Computational power (GPGPUs)
Deep Learning "Trick": Pre-training
Deep Learning "Trick": Dropout
Before presenting each training example and performing backprop, randomly ignore 50% of the nodes in your network.
http://www.jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf
Deep Learning "Trick": ReLUs
- May not need pre-training or dropout.
Aside: Convolution
Convolutional Neural Network (HTF 11.7)
Want to give it a try?
(Other packages available.)
- Be prepared to:
- Search for and read papers
- Try different architectures
- Try different training methods
- Wait (depending on your network size/training set size)
Deep Learning Resources (also on wiki)
Tutorials on Word2Vec in Python. Learns semantic relationships between words in very large corpora by mapping each word to a high-dimensional word embedding. Semantic relationships are estimated using contextual frequency, i.e. how often a word appears given a context of other words.
https://radimrehurek.com/gensim/models/word2vec.html
https://rare-technologies.com/word2vec-tutorial/
Some ideas about using t-SNE for visualization
https://www.jeffreythompson.org/blog/2017/02/13/using-word2vec-and-tsne/
Digit classification on MNIST dataset using TensorFlow
Deep learning resources (cont'd)
Autoencoders for MNIST in Keras (a very high level interface for deep learning libraries including TensorFlow)
https://blog.keras.io/building-autoencoders-in-keras.html
Convolutional neural networks for image recognition on CIFAR-10 dataset in TensorFlow. Great starting point for image classification using deep learning.
Instance-based learning, Decision Trees
Non-parametric learning
\(k\)-nearest neighbour
Efficient implementations
Variations
Parametric supervised learning
So far, we have assumed that we have a data set \(D\) of labeled examples
From this, we learn a parameter vector of a fixed size such that some error measure based on the training data is minimized
These methods are called parametric, and their main goal is to summarize the data using the parameters
Parametric methods are typically global, i.e. have one set of parameters for the entire data space
But what if we just remembered the data?
When new instances arrive, we will compare them with what we know, and determine the answer
Non-parametric (memory-based) learning methods
Key idea: just store all training examples \(\langle {\mathbf{x}}_i, y_i\rangle\)
When a query is made, compute the value of the new instance based on the values of the closest (most similar) points
Requirements:
A distance function
How many closest points (neighbors) to look at?
How do we compute the value of the new point based on the existing values?
Simple idea: Connect the dots!
Simple idea: Connect the dots!
One-nearest neighbor
Given: Training data \(\{({\mathbf{x}}_i,y_i)\}_{i=1}^n\), distance metric \(d\) on \({{\cal X}}\).
Training: Nothing to do! (just store data)
Prediction: for \({\mathbf{x}}\in{{\cal X}}\)
Find nearest training sample to \({\mathbf{x}}\).
\[i^*\in\arg\min_id({\mathbf{x}}_i,{\mathbf{x}})\]Predict \(y=y_{i^*}\).
What does the approximator look like?
- Nearest-neighbor does not explicitly compute decision boundaries
- But the effective decision boundaries are a subset of the Voronoi diagram for the training data
Each line segment is equidistant between two points of opposite classes.
What kind of distance metric?
Euclidian distance
Maximum/minimum difference along any axis
Weighted Euclidian distance (with weights based on domain knowledge) \[d({\bf x}, {\bf x'})=\sum_{j=1}^p u_j ({x}_j - {x'}_j)^2\]
An arbitrary distance or similarity function \(d\), specific for the application at hand (works best, if you have one)
Distance metric is really important!
Left: attributes weighted equally Right: unequal weighting
Distance metric tricks
You may need to do preprocessing:
Scale the input dimensions (or normalize them)
Remove noisy inputs
Determine weights for attributes based on cross-validation (or information-theoretic methods)
Distance metric is often domain-specific
E.g. string edit distance in bioinformatics
E.g. trajectory distance in time series models for walking data
Distance metric can be learned sometimes (more on this later)
\(k\)-nearest neighbor
Given: Training data \(\{({\mathbf{x}}_i,y_i)\}_{i=1}^n\), distance metric \(d\) on \({{\cal X}}\).
Learning: Nothing to do!
Prediction: for \({\mathbf{x}}\in{{\cal X}}\)
Find the \(k\) nearest training samples to \({\mathbf{x}}\).
Let their indices be \(i_1, i_2, \ldots, i_k\).Predict
\(y=\) mean/median of \(\{y_{i_1},y_{i_2},\ldots, y_{i_k}\}\) for regression
\(y=\) majority of \(\{y_{i_1},y_{i_2},\ldots, y_{i_k}\}\) for classification, or empirical probability of each class
k-NN classification, Majority, k=1
k-NN classification, Majority, k=2
k-NN classification, Majority, k=3
k-NN classification, Majority, k=5
k-NN classification, Majority, k=10
k-NN classification, Majority, k=15
k-NN classification, Mean (prob), k=1
k-NN classification, Mean (prob), k=2
k-NN classification, Mean (prob), k=3
k-NN classification, Mean (prob), k=5
k-NN classification, Mean (prob), k=10
k-NN classification, Mean (prob), k=15
k-NN classification, Mean (prob), k=20
k-NN classification, Mean (prob), k=25
k-NN regression, Mean, k=1
k-NN regression, Mean, k=2
k-NN regression, Mean, k=3
k-NN regression, Mean, k=5
k-NN regression, Mean, k=10
k-NN regression, Mean, k=15
k-NN regression, Mean, k=20
k-NN regression, Mean, k=25
Bias-variance trade-off
If \(k\) is low, very non-linear functions can be approximated, but we also capture the noise in the data
Bias is low, variance is highIf \(k\) is high, the output is much smoother, less sensitive to data variation
High bias, low varianceA validation set can be used to pick the best \(k\)
Locally-weighted regression
- Weighted regression: different weights in the error function for different points
\[ J({\mathbf{w}}) = \sum_i w_i \cdot (h_{\mathbf{w}}({\mathbf{x}}_i) - y_i)^2 \]
- Locally weighted regression: weights depend on the distance to the query point
LOESS Smoothing
- Quadratic Regression
- Uses the closest \(\alpha\) percent of the training set to make each prediction, called "span"
LOESS Smoothing, alpha=0.200
LOESS Smoothing, alpha=0.300
LOESS Smoothing, alpha=0.400
LOESS Smoothing, alpha=0.500
LOESS Smoothing, alpha=0.600
LOESS Smoothing, alpha=0.700
LOESS Smoothing, alpha=0.750
LOESS Smoothing, alpha=0.800
LOESS Smoothing, alpha=0.900
LOESS Smoothing, alpha=1.000
Generalized Additive Models
- Also smooth functions of the input variables; appearance similar to LOESS but with deeper theory.
- Based on regression splines
GAM Smoothed Example
Lazy and eager learning
Lazy: wait for query before generalizing
E.g. Nearest Neighbor
Eager: generalize before seeing query
E.g. SVM, Linear regression
Does it matter?
Pros and cons of lazy and eager learning
Eager learners must create global approximation
Lazy learners can create many local approximations
An eager learner does the work off-line, summarizes lots of data with few parameters
A lazy learner has to do lots of work sifting through the data at query time
Typically lazy learners take longer time to answer queries and require more space
When to consider nonparametric methods
- When you have: instances that map to points in \({\mathbb R}^p\), not too many attributes per instance (\(< 20\)), lots of data
|
|
Decision Trees
What are decision trees?
Methods for constructing decision trees
Overfitting avoidance
Non-metric learning
The result of learning is not a set of parameters, but there is no distance metric to assess similarity of different instances
Typical examples:
Decision trees
Rule-based systems
Example: Decision tree for Wisconsin data
Internal nodes are tests on the values of different attributes
Tests can be binary or multi-valued
Each training example \(\langle{\mathbf{x}}_i,y_i\rangle\) falls in precisely one leaf.
Using decision trees for classification
How do we classify a new a new instance, e.g.: radius=18, texture=12, …
At every node, test the corresponding attribute
Follow the appropriate branch of the tree
At a leaf, one can predict the class of the majority of the examples for the corresponding leaf, or the probabilities of the two classes.
Decision trees as logical representations
A decision tree can be converted an equivalent set of if-then rules.
| IF | THEN most likely class is |
|---|---|
| radius \(>17.5\) AND texture \(>21.5\) | R |
| radius \(>17.5\) AND texture \(\leq 21.5\) | N |
| radius \(\leq17.5\) | N |
Decision trees as logical representations
A decision tree can be converted an equivalent set of if-then rules.
| IF | THEN P(R) is |
|---|---|
| radius\(> 17.5\) AND texture\(> 21.5\) | \(33/(33+5)\) |
| radius\(> 17.5\) AND texture\(\leq 21.5\) | \(12/(12+31)\) |
| radius\(\leq 17.5\) | \(25/(25+64)\) |
Decision trees, more formally
Each internal node contains a test, on the value of one (typically) or more feature values
A test produces discrete outcomes, e.g.,
radius \(> 17.5\)
radius \(\in [12,18]\)
grade is \(\in \{A,B,C\}\)
color is RED
For discrete features, typically branch on some, or all, possible values
For real features, typically branch based on a threshold value
A finite set of possible tests is usually decided before learning the tree; learning comprises choosing the shape of the tree and the tests at every node.
More on tests for real-valued features
Suppose feature \(j\) is real-valued,
How do we choose a finite set of possible thresholds, for tests of the form \(x_j > \tau\)?
Regression: choose midpoints of the observed data values, \(x_{1,j}, x_{2,j}, \ldots, x_{m,j}\)
Classification: choose midpoints of data values with different \(y\) values
Representational power and efficiency of decision trees
Suppose the input \({\bf x}\) consists of \(n\) binary features
How can a decision tree represent:
\(y = x_1\) AND \(x_2\) AND … AND \(x_n\)
\(y = x_1\) OR \(x_2\) OR … OR \(x_n\)
\(y = x_1\) XOR \(x_2\) XOR … XOR \(x_n\)
Representational power and efficiency of decision trees
With typical univariate tests, AND and OR are easy, taking \(O(n)\) tests
Parity/XOR type problems are hard, taking \(O(2^n)\) tests
With real-valued features, decision trees are good at problems in which the class label is constant in large, connected, axis-orthogonal regions of the input space.
An artificial example
Example: Decision tree decision surface
How do we learn decision trees?
Usually, decision trees are constructed in two phases:
An recursive, top-down procedure "grows" a tree
(possibly until the training data is completely fit)The tree is "pruned" back to avoid overfitting
Both typically use greedy heuristics
Top-down induction of decision trees
For a classification problem:
If all the training instances have the same class, create a leaf with that class label and exit.
Pick the best test to split the data on
Split the training set according to the value of the outcome of the test
Recurse on each subset of the training data
Top-down induction of decision trees
For a regression problem - same as above, except:
The decision on when to stop splitting has to be made earlier
At a leaf, either predict the mean value, or do a linear fit
Which test is best?
The test should provide information about the class label.
Suppose we have 30 positive examples, 10 negative ones, and we are considering two tests that would give the following splits of instances:
Which test is best?
Intuitively, we would like an attribute that separates the training instances as well as possible
If each leaf was pure, the attribute would provide maximal information about the label at the leaf
We need a mathematical measure for the purity of a set of instances
Entropy
\[H(P)=\sum_{i=1}^k p_i \log_2\frac{1}{p_i}\]
- The further \(P\) is from uniform, the lower the entropy
Entropy applied to binary classfication
Consider data set \(D\) and let
\(p_{\oplus}=\) the proportion of positive examples in \(D\)
\(p_{\ominus}=\) the proportion of negative examples in \(D\)
Entropy measures the impurity of \(D\), based on empirical probabilities of the two classes: \[H(D) \equiv p_{\oplus} \log_{2} \frac{1}{p_{\oplus}} + p_{\ominus} \log_{2} \frac{1}{p_{\ominus}}\]
Marginal Entropy
|
|
Specific Conditional entropy
|
Specific conditional entropy is the uncertainty in \(Y\) given a particular \(x\) value. E.g.,
|
(Average) Conditional entropy
|
|
Information gain
How much does the entropy of \(Y\) go down, on average, if I am told the value of \(X\)? \[IG(Y|X)=E[H(Y)-H(Y|X)]\] This is called information gain
Alternative interpretation: what reduction in entropy would be obtained by knowing \(X\)
Intuitively, this has the meaning we seek for decision tree construction
Information gain to determine best test
- We choose, recursively at each interior node, the test that has highest empirical information gain (on the training set.)
- If tests are binary:
\[\begin{aligned} IG(D,\mbox{Test}) & = H(D) - H(D|\mbox{Test}) \\ & = H(D) - \frac{|D_{\mbox{Test}}|}{|D|} H(D_{\mbox{Test}}) - \frac{|D_{\lnot \mbox{Test}}|}{|D|} H(D_{\lnot \mbox{Test}}) \end{aligned}\]
(Can check that in this case, the test on the left has higher IG.)
Caveats on tests with multiple values
If the outcome of a test is multi-valued, the number of possible values influences the information gain
The more possible values, the higher the gain! (the more likely it is to form small, but pure partitions)
C4.5 (one famous decision tree construction algorithm) uses only binary tests:
Attribute \(=\) Value for discrete attributes
Attribute \(<\) or \(>\) Value for continuous attributes
Other approaches consider smarter metrics (e.g. gain ratio), which account for the number of possible outcomes
Dealing with noise in the training data
Noise is inevitable!
Values of attributes can be misrecorded
Values of attributes may be missing
The class label can be misrecorded
What happens when adding a noisy example?
Overfitting in decision trees
Remember, decision tree construction proceeds until all leaves are pure – all examples having the same \(y\) value.
As the tree grows, the generalization performance starts to degrade, because the algorithm is finding irrelevant tests.
Example from (Mitchell, 1997)
Avoiding overfitting
Two approaches:
Stop growing the tree when further splitting the data does not yield a statistically significant improvement
Grow a full tree, then prune the tree, by eliminating nodes
The second approach has been more successful in practice, because in the first case it might be hard to decide if the information gain is sufficient or not (e.g. for multivariate functions)
We will select the best tree, for now, by measuring performance on a separate validation data set.
Example: Reduced-error pruning
Split the “training data” into a training set and a validation set
Grow a large tree (e.g. until each leaf is pure)
For each node:
Evaluate the validation set accuracy of pruning the subtree rooted at the node
Greedily remove the node that most improves validation set accuracy, with its corresponding subtree
Replace the removed node by a leaf with the majority class of the corresponding examples.
Stop when pruning starts hurting the accuracy on the validation set.
Example: Effect of reduced-error pruning
Example: Rule post-pruning in C4.5
Convert the decision tree to rules
Prune each rule independently of the others, by removing preconditions such that the accuracy is improved
Sort final rules in order of estimated accuracy
Advantages:
Can prune attributes higher up in the tree differently on different paths
There is no need to reorganize the tree if pruning an attribute that is higher up
Often people want rules anyway, for readability
Random Forests
Draw \(B\) bootstrapped datasets, learn \(B\) decision trees.
Average/vote the outputs.
When choosing each split, only consider a random \(\sqrt{p}\)-sized subset of the features.
Prevents overfitting
Works extremely well
Missing values during classification
Assign “most likely” value based on all the data that reaches the current node. This is a form of .
Assign all possible values with some probability.
Count the occurrences of the different attribute values in the instances that have reached the same node.
Predict all the possible class labels with the appropriate probabilities
Introduce a value that means “unknown”
Decision Tree Summary (1)
Very fast learning algorithms (e.g. C4.5, CART)
Attributes may be discrete or continuous, no preprocessing needed
Provide a general representation of classification rules
Easy to understand! Though…
Exact tree output may be sensitive to small changes in data
With many features, tests may not be meaningful
Decision Tree Summary (2)
In standard form, good for (nonlinear) piecewise axis-orthogonal decision boundaries – not good with smooth, curvilinear boundaries
In regression, the function obtained is discontinuous, which may not be desirable
Good accuracy in practice – many applications
Extra Slides
What is information?
Imagine:
You are about to observe the outcome of a dice roll
You are about to observe the outcome of a coin flip
You are about to observe the outcome of a biased coin flip
Someone is about to tell you your own name
Intuitively, in each situation you have a different amount of uncertainty as to what outcome / message you will observe.
Information = Reduction in uncertainty
Let \(E\) be an event that occurs with probability \(P(E)\). If we are told that \(E\) has occurred with certainty, then we received \[I(E) = \log_2\frac{1}{P(E)}\] bits of information.
You can also think of information as the amount of “surprise” in the outcome (e.g., consider \(P(E)=1\), \(P(E)\approx 0\))
E.g., result of a fair coin flip provides \(\log_2 2 = 1\) bit of information
E.g., result of a fair dice roll provides \(\log_2 6 \approx 2.58\) bits of information.
E.g., result of being told your own name (or any other deterministic event) produces \(0\) bits of information
Interpretations of entropy
\[H(P) = \sum_i p_i \log_2\frac{1}{p_i}\]
Average amount of information per symbol
Average amount of surprise when observing the symbol
Uncertainty the observer has before seeing the symbol
Average number of bits needed to communicate the symbol
Alternative purity measures
For classification, an alternative to the information gain is the
Gini index: \[\sum_y P(y)(1-P(y)) = 1-\sum_y (P(y))^2\] Same qualitative behavior as the entropy, but not the same interpretationFor regression trees, purity is measured by the average mean-squared error at each leaf
E.g. CART (Breiman et al., 1984)









