 \includegraphics{images/NoSep_RBFSVM}
## Second brush with “feature construction”
- With polynomial regression, we saw how to construct features to
increase the size of the hypothesis space
- This gave more flexible regression functions
- Kernels offer a similar function with SVMs: More flexible decision
boundaries
- Often not clear what kernel is appropriate for the data at hand; can choose using validation set
## SVM Summary
- Linear SVMs find a maximum margin linear separator between the classes
- If classes are not linearly separable,
- Use the soft-margin formulation to allow for errors
- Use a kernel to find a boundary that is non-linear
- Or both (usually both)
- Choosing the soft margin parameter C and choosing the kernel and any kernel parameters must be done using validation (not training)
## Getting SVMs to work in practice
- `libsvm` and `liblinear` are popular
- Scaling the inputs ($\x_i$) is very important. (E.g. make all mean zero variance 1.)
- Two important choices:
- Kernel (and kernel parameters, e.g. $\gamma$ for the RBF kernel)
- Regularization parameter $C$
- The parameters may interact -- best $C$ may depend on $\gamma$
- Together, these control overfitting: best to do a *within-fold
parameter search, using a validation set*
- Clues you might be overfitting: Low margin (large weights), Large fraction of instances are support vectors
## Kernels beyond SVMs
- Remember, a kernel is a special kind of similarity measure
- A lot of research has to do with defining new kernel
functions, suitable to particular tasks / kinds of input objects
- Many kernels are available:
- Information diffusion kernels (Lafferty and Lebanon, 2002)
- Diffusion kernels on graphs (Kondor and Jebara 2003)
- String kernels for text classification (Lodhi et al, 2002)
- String kernels for protein classification (e.g., Leslie et
al, 2002)
... and others!
## Instance-based learning, Decision Trees
- Non-parametric learning
- $k$-nearest neighbour
- Efficient implementations
- Variations
## Parametric supervised learning
- So far, we have assumed that we have a data set $D$ of labeled
examples
- From this, we learn a *parameter vector* of a
*fixed size* such that some error measure based on the
training data is minimized
- These methods are called *parametric*, and their main
goal is to summarize the data using the parameters
- Parametric methods are typically global, i.e. have one set of
parameters for the entire data space
- But what if we just remembered the data?
- When new instances arrive, we will compare them with what we know,
and determine the answer
## Non-parametric (memory-based) learning methods
- Key idea: just store all training examples
$\langle \x_i, y_i\rangle$
- When a query is made, compute the value of the new instance based on
the values of the *closest (most similar) points*
- Requirements:
- A distance function
- How many closest points (neighbors) to look at?
- How do we compute the value of the new point based on the
existing values?
## Simple idea: Connect the dots!
```{r echo=F,message=F,fig.height=6,fig.width=8}
library(ggplot2);library(dplyr);library(class)
testx <- sort(bc$Radius.Mean)
#Add points a little bit on either side of midpoints as test points
testx <- sort(c(testx,rowMeans(embed(testx,2)) + 0.00001,rowMeans(embed(testx,2)) - 0.00001))
test <- data.frame(x=testx)
bctest <- data.frame(Radius.Mean=test$x)
test$y <- as.numeric(class::knn(bc[,'Radius.Mean'],bctest,bc$Outcome)) - 1
bc <- bc %>% mutate(binOutcome = as.numeric(Outcome == "R"))
ggplot(bc,aes(x=Radius.Mean,y=binOutcome)) + geom_point(aes(colour=Outcome)) + geom_line(data=test,aes(x=x,y=y))
```
## Simple idea: Connect the dots!
```{r echo=F,message=F,fig.height=6,fig.width=8}
library(ggplot2);library(dplyr);library(caret)
bcr <- filter(bc,Outcome=="R")
testx <- sort(bcr$Radius.Mean)
#Add points a little bit on either side of midpoints as test points
testx <- sort(c(testx,rowMeans(embed(testx,2)) + 0.00001,rowMeans(embed(testx,2)) - 0.00001))
test <- data.frame(x=testx)
bctest <- data.frame(Radius.Mean=test$x)
test$y <- knnregTrain(bcr[,'Radius.Mean'],bctest,bcr$Time,k=1)
ggplot(bcr,aes(x=Radius.Mean,y=Time)) + geom_point(colour="#00BFC4") + geom_line(data=test,aes(x=x,y=y))
```
## One-nearest neighbor
- Given: Training data
$\{(\x_i,y_i)\}_{i=1}^n$, distance metric $d$
on ${{\cal X}}$.
- Training: Nothing to do! (just store data)
- Prediction: for $\x\in{{\cal X}}$
- Find nearest training sample to $\x$.\
$$i^*\in\arg\min_id(\x_i,\x)$$
- Predict $y=y_{i^*}$.
## What does the approximator look like?
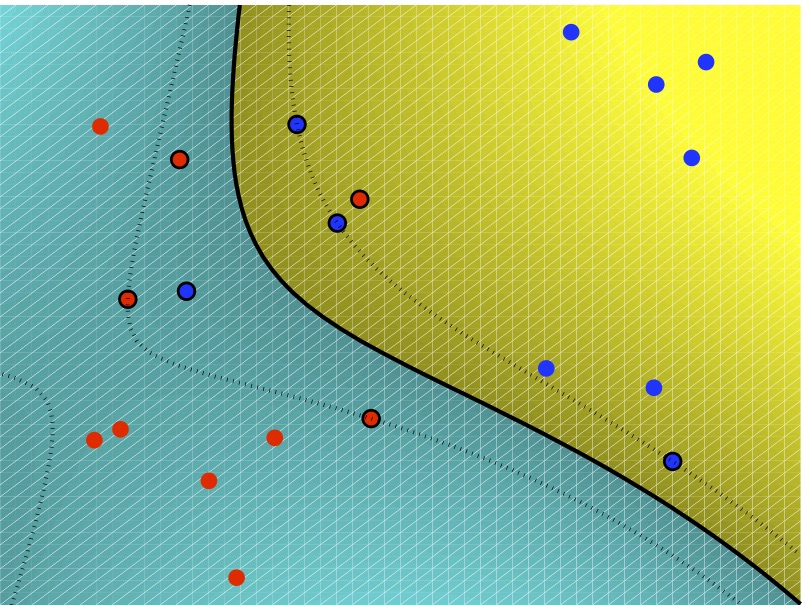
- Nearest-neighbor does not explicitly compute decision boundaries
- But the effective decision boundaries are a subset of the
*Voronoi diagram* for the training data
\includegraphics{images/NoSep_RBFSVM}
## Second brush with “feature construction”
- With polynomial regression, we saw how to construct features to
increase the size of the hypothesis space
- This gave more flexible regression functions
- Kernels offer a similar function with SVMs: More flexible decision
boundaries
- Often not clear what kernel is appropriate for the data at hand; can choose using validation set
## SVM Summary
- Linear SVMs find a maximum margin linear separator between the classes
- If classes are not linearly separable,
- Use the soft-margin formulation to allow for errors
- Use a kernel to find a boundary that is non-linear
- Or both (usually both)
- Choosing the soft margin parameter C and choosing the kernel and any kernel parameters must be done using validation (not training)
## Getting SVMs to work in practice
- `libsvm` and `liblinear` are popular
- Scaling the inputs ($\x_i$) is very important. (E.g. make all mean zero variance 1.)
- Two important choices:
- Kernel (and kernel parameters, e.g. $\gamma$ for the RBF kernel)
- Regularization parameter $C$
- The parameters may interact -- best $C$ may depend on $\gamma$
- Together, these control overfitting: best to do a *within-fold
parameter search, using a validation set*
- Clues you might be overfitting: Low margin (large weights), Large fraction of instances are support vectors
## Kernels beyond SVMs
- Remember, a kernel is a special kind of similarity measure
- A lot of research has to do with defining new kernel
functions, suitable to particular tasks / kinds of input objects
- Many kernels are available:
- Information diffusion kernels (Lafferty and Lebanon, 2002)
- Diffusion kernels on graphs (Kondor and Jebara 2003)
- String kernels for text classification (Lodhi et al, 2002)
- String kernels for protein classification (e.g., Leslie et
al, 2002)
... and others!
## Instance-based learning, Decision Trees
- Non-parametric learning
- $k$-nearest neighbour
- Efficient implementations
- Variations
## Parametric supervised learning
- So far, we have assumed that we have a data set $D$ of labeled
examples
- From this, we learn a *parameter vector* of a
*fixed size* such that some error measure based on the
training data is minimized
- These methods are called *parametric*, and their main
goal is to summarize the data using the parameters
- Parametric methods are typically global, i.e. have one set of
parameters for the entire data space
- But what if we just remembered the data?
- When new instances arrive, we will compare them with what we know,
and determine the answer
## Non-parametric (memory-based) learning methods
- Key idea: just store all training examples
$\langle \x_i, y_i\rangle$
- When a query is made, compute the value of the new instance based on
the values of the *closest (most similar) points*
- Requirements:
- A distance function
- How many closest points (neighbors) to look at?
- How do we compute the value of the new point based on the
existing values?
## Simple idea: Connect the dots!
```{r echo=F,message=F,fig.height=6,fig.width=8}
library(ggplot2);library(dplyr);library(class)
testx <- sort(bc$Radius.Mean)
#Add points a little bit on either side of midpoints as test points
testx <- sort(c(testx,rowMeans(embed(testx,2)) + 0.00001,rowMeans(embed(testx,2)) - 0.00001))
test <- data.frame(x=testx)
bctest <- data.frame(Radius.Mean=test$x)
test$y <- as.numeric(class::knn(bc[,'Radius.Mean'],bctest,bc$Outcome)) - 1
bc <- bc %>% mutate(binOutcome = as.numeric(Outcome == "R"))
ggplot(bc,aes(x=Radius.Mean,y=binOutcome)) + geom_point(aes(colour=Outcome)) + geom_line(data=test,aes(x=x,y=y))
```
## Simple idea: Connect the dots!
```{r echo=F,message=F,fig.height=6,fig.width=8}
library(ggplot2);library(dplyr);library(caret)
bcr <- filter(bc,Outcome=="R")
testx <- sort(bcr$Radius.Mean)
#Add points a little bit on either side of midpoints as test points
testx <- sort(c(testx,rowMeans(embed(testx,2)) + 0.00001,rowMeans(embed(testx,2)) - 0.00001))
test <- data.frame(x=testx)
bctest <- data.frame(Radius.Mean=test$x)
test$y <- knnregTrain(bcr[,'Radius.Mean'],bctest,bcr$Time,k=1)
ggplot(bcr,aes(x=Radius.Mean,y=Time)) + geom_point(colour="#00BFC4") + geom_line(data=test,aes(x=x,y=y))
```
## One-nearest neighbor
- Given: Training data
$\{(\x_i,y_i)\}_{i=1}^n$, distance metric $d$
on ${{\cal X}}$.
- Training: Nothing to do! (just store data)
- Prediction: for $\x\in{{\cal X}}$
- Find nearest training sample to $\x$.\
$$i^*\in\arg\min_id(\x_i,\x)$$
- Predict $y=y_{i^*}$.
## What does the approximator look like?
- Nearest-neighbor does not explicitly compute decision boundaries
- But the effective decision boundaries are a subset of the
*Voronoi diagram* for the training data
| - Advantages: - Training is very fast - Easy to learn complex functions over few variables - Can give back confidence intervals in addition to the prediction - *Often wins* if you have enough data | - Disadvantages: - Slow at query time - Query answering complexity depends on the number of instances - *Easily fooled by irrelevant attributes* (for most distance metrics) - "Inference" is not possible |
| $x=$HasKids $y=$OwnsFrozenVideo ------------- ------------------- Yes Yes Yes Yes Yes Yes Yes Yes No No No No Yes No Yes No | - From the table, we can estimate $P(Y=\mathrm{Yes}) = 0.5 = P(Y=\mathrm{No})$. - Thus, we estimate $H(Y) = 0.5 \log \frac{1}{0.5} + 0.5 \log \frac{1}{0.5} = 1$. |
| $x=$HasKids $y=$OwnsFrozenVideo ------------- ------------------- Yes Yes Yes Yes Yes Yes Yes Yes No No No No Yes No Yes No | *Specific conditional entropy* is the uncertainty in $Y$ given a particular $x$ value. E.g., - $P(Y=\mathrm{Yes}|X=\mathrm{Yes}) = \frac{2}{3}$, $P(Y=\mathrm{No}|X=\mathrm{Yes})=\frac{1}{3}$ - $H(Y|X=\mathrm{Yes}) = \frac{2}{3}\log \frac{1}{(\frac{2}{3})} + \frac{1}{3}\log \frac{1}{(\frac{1}{3})}$ $\approx 0.9183$. |
| $x=$HasKids $y=$OwnsFrozenVideo ------------- ------------------- Yes Yes Yes Yes Yes Yes Yes Yes No No No No Yes No Yes No | - *The conditional entropy, $H(Y|X)$*, is the specific conditional entropy of $y$ averaged over the values for $x$: $$H(Y|X)=\sum_x P(X=x)H(Y|X=x)$$ - $H(Y|X=\mathrm{Yes}) = \frac{2}{3}\log \frac{1}{(\frac{2}{3})} + \frac{1}{3}\log \frac{1}{(\frac{1}{3})}$ $\approx 0.9183$ - $H(Y|X=\mathrm{No}) = 0 \log \frac{1}{0} + 1 \log \frac{1}{1} = 0$. - $H(Y|X) = H(Y|X=\mathrm{Yes})P(X=\mathrm{Yes}) + H(Y|X=\mathrm{No})P(X=\mathrm{No})$ $= 0.9183 \cdot \frac{3}{4} + 0 \cdot \frac{1}{4}$ $\approx 0.6887$ - Interpretation: the expected number of bits needed to transmit $y$ if both the emitter and the receiver know the possible values of $x$ (but before they are told $x$’s specific value). |