| ```{r echo=F,results='asis'} library(knitr) exb <- ex names(exb) <- c("x0","x1","y") kable(exb) ``` | Models will be of the form $$ \begin{align} h_\w(\x) & = x_0 w_0 + x_1 w_1\\ & = w_0 + x_1 w_1 \end{align} $$ *How should we pick $\w$?* |
| ```{r echo=F,results='asis'} library(knitr) exb <- ex names(exb) <- c("x0","x1","y") kable(exb) ``` | ```{r fig.width=6,echo=F,message=F} ggplot(exb,aes(x=x1,y=y)) + geom_point(size=4) + geom_smooth(method="lm",formula=y ~ x,se=F,n=200,na.rm=F) #mod <- lm(y ~ x1, data=exb); print(mod$coefficients) ``` $h_{\bf w} ({\bf x}) = 1.06 + 1.61 x_1$ |
| ```{r fig.width=4,echo=F} f9 ``` | - Training error of the degree-9 polynomial is 0. - Training error of the degree-9 polynomial *on any set of 10 points* is 0. |
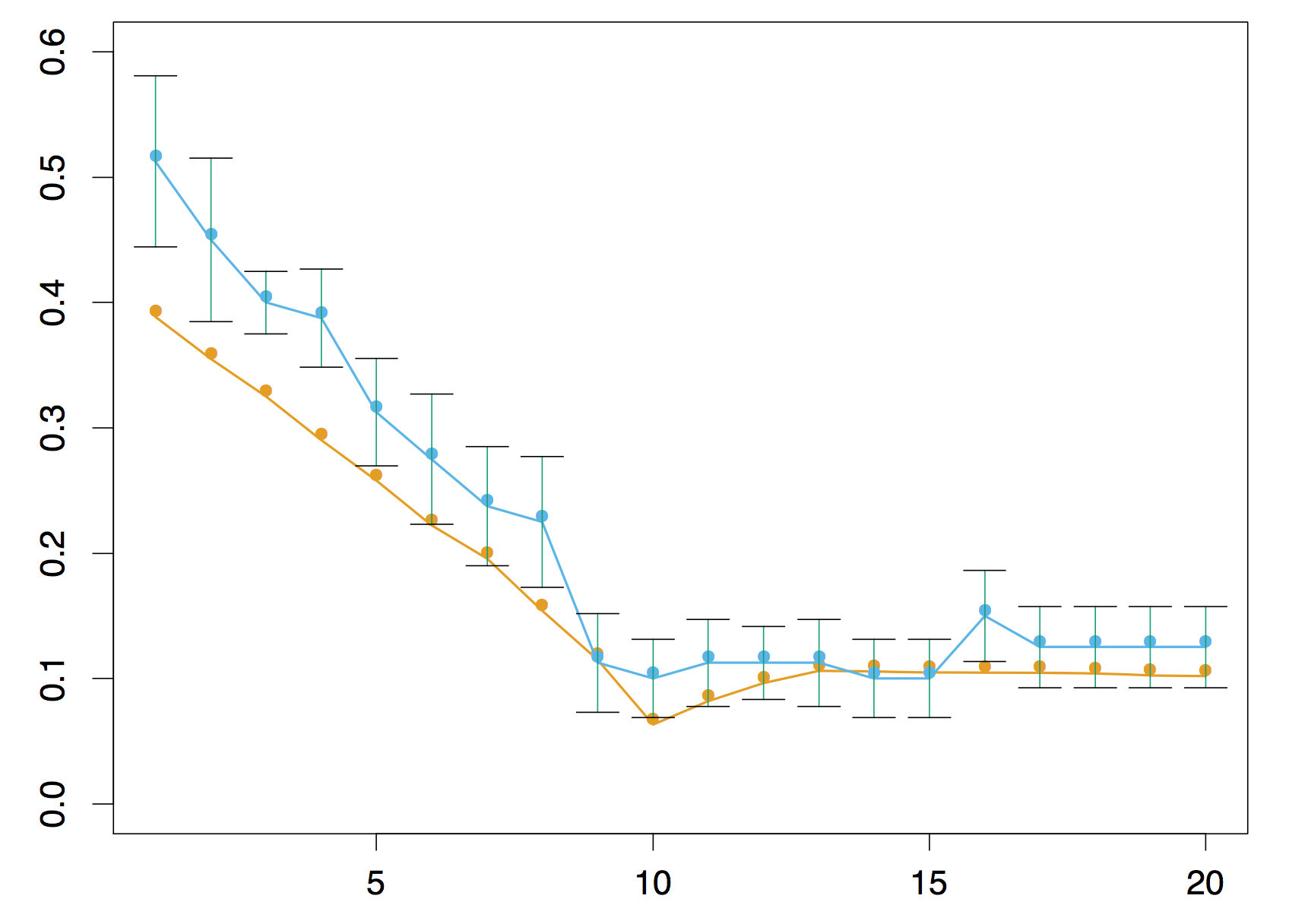 ## Estimating "which is best"
## Estimating "which is best" 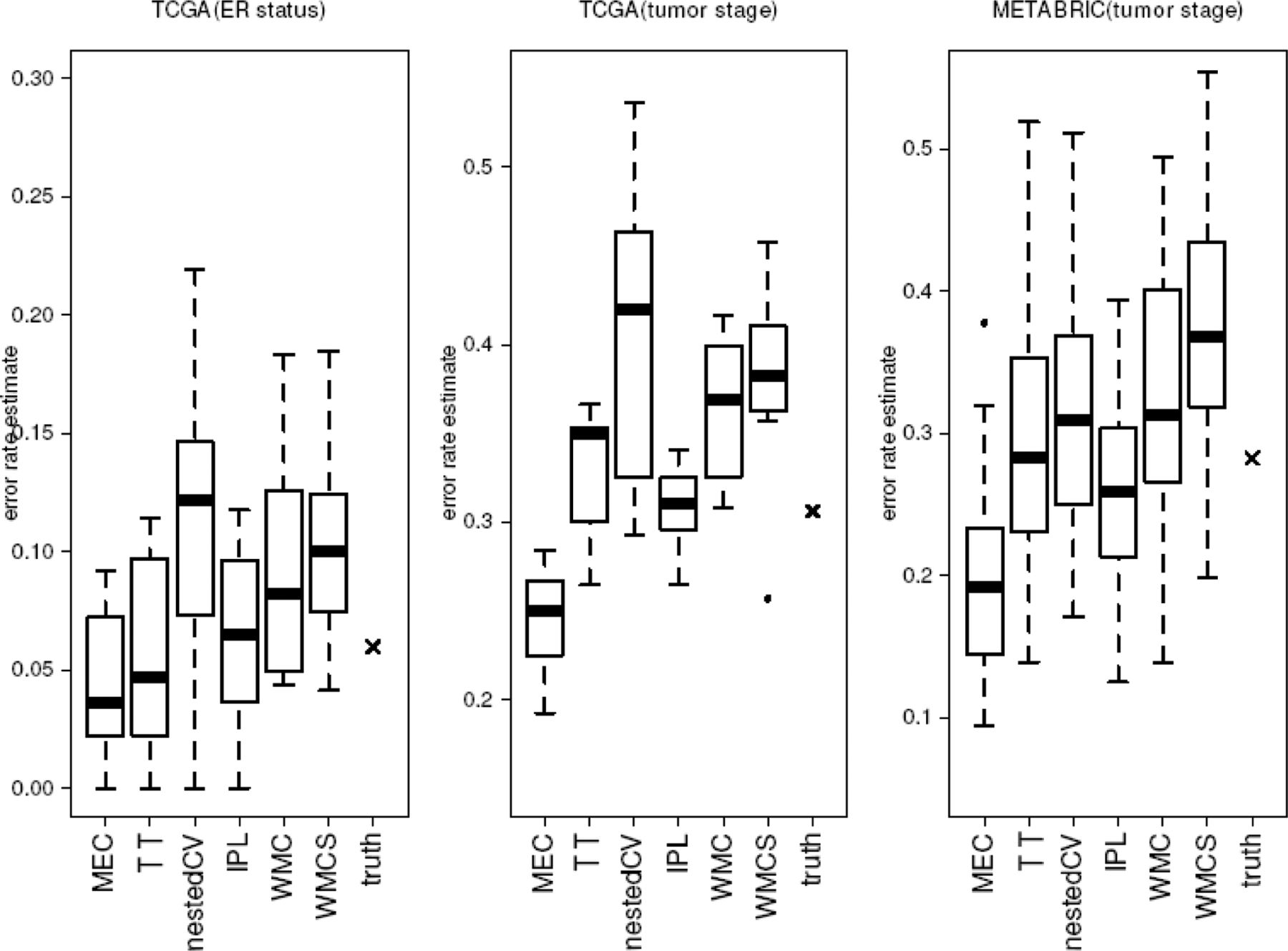 [Estimated errors using 290 model spaces.](http://bioinformatics.oxfordjournals.org/content/30/22/3152.long)
## Nested CV for Model Evaluation {.smaller}
- Divide the instances into $k$ "outer" folds of size $n/k$.
- Loop over the $k$ outer folds $i = 1 ... k$:
- Fold $i$ is for testing; all others for training.
- Divide the training instances into $k'$ "inner" folds of size $(n - n/k)/k'$.
- Loop over $m$ model spaces $1 ... m$
- Loop over the $k'$ inner folds $j = 1 ... k'$:
- Fold $j$ is for validation
- The rest are used for training
- Use average error over folds and SE to choose model space.
- Train on all inner folds.
- Test the model on outer test fold
## Nested CV for Model Evaluation
```{r echo=F,fig.height=6,fig.width=8.5}
library(cvTools)
set.seed(1)
processtestfold <- function(i) {
trange <- ((i-1)*fsize + 1):(i*fsize)
tf <- train[trange,] #Test fold
tr <- train[c(-trange),]
thefolds <- cvFolds(nrow(tr), K = folds, R = 1)
valerr <- NULL
for (deg in 1:min(dmax,nrow(tr)-1)) {
thecall <- call("lm",formula=y~poly(x,deg))
valerr[deg] <- cvTool(call=thecall,data=tr,y=tr$y,folds=thefolds)
}
dstar <- which.min(valerr)
modstar <- lm(y~poly(x,dstar),data=tr)
testerr <- mean((tf$y - predict(modstar,tf))^2)
plt <- ggplot(tr,aes(x=x,y=y)) + geom_point(color="red",size=2) + geom_point(data=tf,color="green3",size=3) +
geom_smooth(data=tr,method="lm",formula=y ~ poly(x,dstar),se=F,n=200,na.rm=F,fullrange=T) +
ggtitle(sprintf("Degree: %d, Error: %.2f",dstar,testerr))
plt$testerr <- testerr
plt
}
ptplots <- lapply(1:folds,processtestfold)
terrors <- sapply(ptplots, function(e) e$testerr)
grid.arrange(grobs=ptplots,top=textGrob(sprintf("Mean MSE: %.2f, SE: %.2f",
mean(terrors),sd(terrors)/sqrt(folds)),gp=gpar(fontsize=20)))
```
## Generalization Error for degree 3 model
```{r echo=F}
dstar <- 3
bestmod <- lm(y~poly(x,dstar),data=train)
testerr <- mean((test$y - predict(bestmod,test))^2)
ggplot(train,aes(x=x,y=y)) + geom_point(color="red",size=2) +
geom_smooth(data=train,method="lm",formula=y ~ poly(x,dstar),se=F,n=200,na.rm=F,fullrange=T) +
ggtitle(sprintf("Degree: %d, Error: %.2f on test set of size 10000",dstar,testerr))
```
Minimum-CV Estimate: 128.48, Nested CV Estimate: 149.91
## Bias-correction for the CV Procedure
[Cawley, Talbot. On Over-fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation. JMLR v.11, 2010.](http://jmlr.org/papers/volume11/cawley10a/cawley10a.pdf)
[Tibshirani, Tibshirani. A bias correction for the minimum error rate in cross-validation. arXiv. 2009.](http://arxiv.org/abs/0908.2904)
[Ding et al. Bias correction for selecting the minimal-error classifier from many machine learning models. Bioinformatics 30 (22). 2014.](http://bioinformatics.oxfordjournals.org/content/30/22/3152.long)
## Summary
- The training error decreases with the degree of the polynomial
$M$, i.e. *the complexity (size) of the model space*
- Generalization error decreases at first, then starts increasing
- Set aside a *validation set* helps us find a good
model space
- We then can report unbiased error estimate, using a *test
set*, **untouched during both parameter training and
validation**
- Cross-validation is a lower-variance but possibly biased version of
this approach. It is standard.
- ***If you have lots of data, just use held-out validation and test sets.***
[Estimated errors using 290 model spaces.](http://bioinformatics.oxfordjournals.org/content/30/22/3152.long)
## Nested CV for Model Evaluation {.smaller}
- Divide the instances into $k$ "outer" folds of size $n/k$.
- Loop over the $k$ outer folds $i = 1 ... k$:
- Fold $i$ is for testing; all others for training.
- Divide the training instances into $k'$ "inner" folds of size $(n - n/k)/k'$.
- Loop over $m$ model spaces $1 ... m$
- Loop over the $k'$ inner folds $j = 1 ... k'$:
- Fold $j$ is for validation
- The rest are used for training
- Use average error over folds and SE to choose model space.
- Train on all inner folds.
- Test the model on outer test fold
## Nested CV for Model Evaluation
```{r echo=F,fig.height=6,fig.width=8.5}
library(cvTools)
set.seed(1)
processtestfold <- function(i) {
trange <- ((i-1)*fsize + 1):(i*fsize)
tf <- train[trange,] #Test fold
tr <- train[c(-trange),]
thefolds <- cvFolds(nrow(tr), K = folds, R = 1)
valerr <- NULL
for (deg in 1:min(dmax,nrow(tr)-1)) {
thecall <- call("lm",formula=y~poly(x,deg))
valerr[deg] <- cvTool(call=thecall,data=tr,y=tr$y,folds=thefolds)
}
dstar <- which.min(valerr)
modstar <- lm(y~poly(x,dstar),data=tr)
testerr <- mean((tf$y - predict(modstar,tf))^2)
plt <- ggplot(tr,aes(x=x,y=y)) + geom_point(color="red",size=2) + geom_point(data=tf,color="green3",size=3) +
geom_smooth(data=tr,method="lm",formula=y ~ poly(x,dstar),se=F,n=200,na.rm=F,fullrange=T) +
ggtitle(sprintf("Degree: %d, Error: %.2f",dstar,testerr))
plt$testerr <- testerr
plt
}
ptplots <- lapply(1:folds,processtestfold)
terrors <- sapply(ptplots, function(e) e$testerr)
grid.arrange(grobs=ptplots,top=textGrob(sprintf("Mean MSE: %.2f, SE: %.2f",
mean(terrors),sd(terrors)/sqrt(folds)),gp=gpar(fontsize=20)))
```
## Generalization Error for degree 3 model
```{r echo=F}
dstar <- 3
bestmod <- lm(y~poly(x,dstar),data=train)
testerr <- mean((test$y - predict(bestmod,test))^2)
ggplot(train,aes(x=x,y=y)) + geom_point(color="red",size=2) +
geom_smooth(data=train,method="lm",formula=y ~ poly(x,dstar),se=F,n=200,na.rm=F,fullrange=T) +
ggtitle(sprintf("Degree: %d, Error: %.2f on test set of size 10000",dstar,testerr))
```
Minimum-CV Estimate: 128.48, Nested CV Estimate: 149.91
## Bias-correction for the CV Procedure
[Cawley, Talbot. On Over-fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation. JMLR v.11, 2010.](http://jmlr.org/papers/volume11/cawley10a/cawley10a.pdf)
[Tibshirani, Tibshirani. A bias correction for the minimum error rate in cross-validation. arXiv. 2009.](http://arxiv.org/abs/0908.2904)
[Ding et al. Bias correction for selecting the minimal-error classifier from many machine learning models. Bioinformatics 30 (22). 2014.](http://bioinformatics.oxfordjournals.org/content/30/22/3152.long)
## Summary
- The training error decreases with the degree of the polynomial
$M$, i.e. *the complexity (size) of the model space*
- Generalization error decreases at first, then starts increasing
- Set aside a *validation set* helps us find a good
model space
- We then can report unbiased error estimate, using a *test
set*, **untouched during both parameter training and
validation**
- Cross-validation is a lower-variance but possibly biased version of
this approach. It is standard.
- ***If you have lots of data, just use held-out validation and test sets.***