

Next: Symbolic Newton Iteration
Up: Advanced Computer Algebra: From Newton
Previous: Division with remainder using Newton
The goal of this section is to formalize in an algebraic
point of view the notions of expansions and approximations
well known in numerical analysis.
Definition 6
Let
R be an Euclidean domain and let
p  R
R be a prime
element.
Let
a  E
E be an element.
We say that
a has
degree zero w.r.t. p and we write
deg(
a,
p) = 0 if for every positive integer
k 

the quotient of
a w.r.t.
pk is zero.
Assume from now on that
a does not have degree zero w.r.t.
p.
If for every positive integer
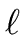
there exists a
positive integer
k >
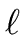
such that
the quotient of
a w.r.t.
pk is not zero,
then we say
a has
infinite degree w.r.t. p and we write
deg(
a,
p) = +
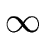
,
otherwise we say that
a has
finite degree w.r.t. p and we write
deg(
a,
p) < +
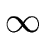
.
Assume furthermore that
deg(
a,
p) < +
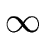
holds.
The largest positive integer
k 

such that the quotient of
a w.r.t.
pk is not zero
is called the
degree of a w.r.t. p and
is denoted by
deg(
a,
p).
Definition 7
The Euclidean size

of an Euclidean domain
R
is said
regular if for every
a,
b  R
R with
b 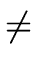
0
there exists a couple
(
q,
r)
 E
E×
E such that
-
a = bq + r,
-
r
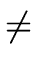 0
0 
 (r) <
(r) <  (b),
(b),
-
q
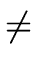 0
0 
 (q) <
(q) <  (a) and
(a) and  (b)
(b) 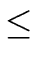
 (a).
(a).
Proposition 8
Let
R be an Euclidean domain with a regular
Euclidean size

.
Let
p be a prime element.
Then for every non-zero
a  E
E there exists
an integer
d  N
N and elements
a0,
a1,...,
ad  E
E such that
-
a = adpd + ... + a1p + a0,
-
ad
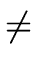 0,
0,
- for every
i = 0 ... d we have
deg(ai, p) = 0.
The sequence
(
a0,
a1,...,
ad) is called
a
p-
adic expansion of
a w.r.t.
p.
Proof.
Let (
q0,
a0) be a couple quotient-remainder
given as in
Definition
7
when dividing
a w.r.t.
p.
First we prove that a0 must have degree 0 w.r.t. p.
This is obvious if a0 = 0.
So let us assume that
a0 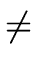 0 holds.
This implies
0 holds.
This implies
 (p) >
(p) >  (a0).
If a0 would have positive degree k w.r.t. p,
then, by the properties of a regular Euclidean size,
we would have
(a0).
If a0 would have positive degree k w.r.t. p,
then, by the properties of a regular Euclidean size,
we would have
 (a0)
(a0) 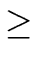
 (pk).
Since
(pk).
Since
 (pk)
(pk) 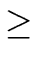
 (p) holds (by definition
of an Euclidean domain) we would have a contradiction
with
(p) holds (by definition
of an Euclidean domain) we would have a contradiction
with
 (p) >
(p) >  (a0).
Therefore in any case we have
deg(a0, p) = 0.
(a0).
Therefore in any case we have
deg(a0, p) = 0.
Next, let us prove the proposition for those elements a
which have quotient 0 w.r.t. p.
Observe that if one quotient of a w.r.t. p is zero
then we have
 (a) <
(a) <  (p).
Hence every quotient of a w.r.t. p is null.
(Otherwise we would have
(p).
Hence every quotient of a w.r.t. p is null.
(Otherwise we would have
 (p)
(p) 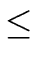
 (a)
by the properties of a regular Euclidean size.)
Since a = a0 and since a0 has degree 0 w.r.t. p,
the element a has degree 0 w.r.t. p and (a0)
is a p-adic expansion of a w.r.t. p.
Therefore the proposition is proved in the case
of the elements a which have quotient 0 w.r.t. p.
(a)
by the properties of a regular Euclidean size.)
Since a = a0 and since a0 has degree 0 w.r.t. p,
the element a has degree 0 w.r.t. p and (a0)
is a p-adic expansion of a w.r.t. p.
Therefore the proposition is proved in the case
of the elements a which have quotient 0 w.r.t. p.
We can assume now that a does not have quotient 0 w.r.t. p
and thus
q0 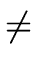 0 and
0 and
 (q0) <
(q0) <  (a) hold.
Then let
(q1, a1) be a couple quotient-remainder
given as in
Definition 7
when dividing q0 w.r.t. p.
If
q1
(a) hold.
Then let
(q1, a1) be a couple quotient-remainder
given as in
Definition 7
when dividing q0 w.r.t. p.
If
q1 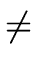 0 then we have
0 then we have
 (q1) <
(q1) <  (q0)
and let
(q2, a2) be a couple quotient-remainder
given as in
Definition 7
when dividing q1 w.r.t. p.
Continuing in this manner we obtain a finite sequence
a0, a1,..., ad
(q0)
and let
(q2, a2) be a couple quotient-remainder
given as in
Definition 7
when dividing q1 w.r.t. p.
Continuing in this manner we obtain a finite sequence
a0, a1,..., ad  R and a finite sequence
q0, q1,..., qd
R and a finite sequence
q0, q1,..., qd  R such that we have
R such that we have
| a |
= |
q0p + a0 |
with |
q0 |
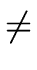 |
0 |
| q0 |
= |
q1p + a1 |
with |
q1 |
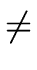 |
0 |
| q1 |
= |
q2p + a2 |
with |
q2 |
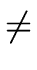 |
0 |
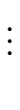 |
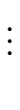 |
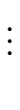 |
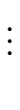 |
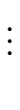 |
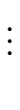 |
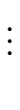 |
| qd2 |
= |
qd-1p + ad-1 |
with |
qd-1 |
 |
0 |
| qd-1 |
= |
qdp + ad |
with |
qd |
= |
0 |
|
|
This process stops since we have
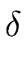 (a) > (a) > 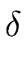 (q0) > (q0) > 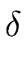 (q1) > (q1) > 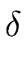 (q2) > ... > (q2) > ... > 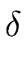 (qd-1) (qd-1) |
(83) |
and since the Euclidean size of an element has value
in

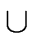
{ -
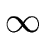
}.
Clearly we have
| a = adpd + ... + a1p + a0. |
|
Moreover
ad =
qd-1 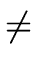
0 holds.
In addition, for every
i = 0
... d we have
deg(
ai,
p) = 0
by the first part of this proof.

Proposition 9
Let
R be a commutative ring with identity element.
Let

 R
R[
y] be a polynomial of degree
n
and let
g  R
R be an element.
We define
p =
y -
g.
There exists a unique sequence
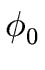
,
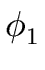
,...,
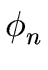
 R
R
such that we have
The above expression is called the
Taylor expansion
of

at
g,
Proof.
By induction on
n.
If
n = 0, the result is clear.
Otherwise let
q and
r be the quotient and the remainder
in the division of

by
p. We have
 = qp + r and r = qp + r and r 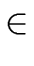 R. R. |
|
Since
r =

(
g) the conclusion
(existence and unicity) follows by the induction hypothesis.

Remark 16
We can characterize the Taylor expansion
of  at g by means of the notion
of a formal derivative.
at g by means of the notion
of a formal derivative.
Definition 8
Let
R be a commutative ring with identity element.
For
we define the
formal derivative of

by
  = = 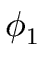 + 2 + 2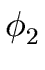 y + ... + n y + ... + n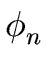 yn-1. yn-1. |
(85) |
Remark 17
The terminology formal derivative comes
from the fact that we do not make use of the notion
of a limit to define this derivative.
Indeed, if R is a finite ring, then this would
not make clear sense.
However we retrieve the usual properties of derivatives.
Proof.
See Lemma 9.19 in [
vzGG99].

Proposition 11
Let
R be a commutative ring with identity element.
Let

 R
R[
y] and let
g  R
R.
There exists a polynomial
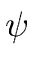
 R
R[
y] such that we have
 (y) = (y) =  (g) + (g) +   (g)(y - g) + (g)(y - g) + 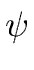 (y)(y - g)2. (y)(y - g)2. |
(86) |
Proof.
Follows easily from
Proposition
9.

Remark 18
Proposition 9
admits several generalizations.
First one can use a monic polynomial p
of degree d > 1.
In this case the coefficients
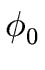 ,
,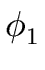 ,...,
,...,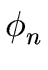 are polynomials of degree less than d.
Another generalization,
given by
Proposition 12,
is for multivariate polynomials.
To understand this generalization, it is important
to make the following three observations.
are polynomials of degree less than d.
Another generalization,
given by
Proposition 12,
is for multivariate polynomials.
To understand this generalization, it is important
to make the following three observations.
- First, in
Proposition 11,
one can consider g as a new indeterminate,
and then the result holds for a polynomial

 R[y, g].
R[y, g].
- Secondly, the notion of a formal derivative
of a univariate polynomial (over a commutative ring
with identity element) leads
naturally to the notion of a partial derivative
of a multivariate polynomial w.r.t. a variable.
We will not detail this here,
since this is quite straightforward
- The quantity
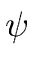 (y - g)2
in Relation (86)
lies in the ideal
(y - g)2
in Relation (86)
lies in the ideal
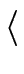 y-g
y-g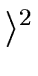 .
.
Proposition 12
Let
R be a commutative ring with identity element.
We consider the ring of multivariate polynomials
P =
R[
x1,...,
xr][
y1,...,
yr].
We define
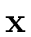
= (
x1,...,
xr)
and
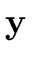
= (
y1,...,
yr).
For every polynomial

 R
R[
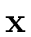
]
there exists a polynomial
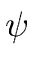
 P
P
lying in the ideal
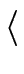 y1
y1,...,
yr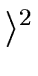
such that
 (x1 + y1,..., xr + yr) = (x1 + y1,..., xr + yr) =  ( (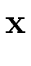 ) + ) + 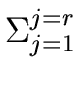 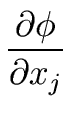 ( (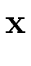 )yj + )yj + 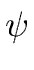 . . |
(87) |
Remark 19
Using the vocabulary of numerical analysis,
Propositions 11
and 12
provides a Taylor expansion of  of order 2.
This leads to the following definition.
of order 2.
This leads to the following definition.
Definition 9
Let
R be a commutative ring with identity element
and let
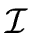
be an ideal of
R.
Let
a,
b  R
R be elements and
k be a positive integer.
We say that
a is an
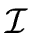
-
adic approximation
of
b at order
k if we have
a  b mod b mod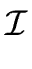 k. k. |
(88) |
Remark 20
We conclude by two useful properties of ideal-adic approximations.
Proposition 13
Let
R be an Euclidean domain with a regular
Euclidean size

.
Let
p  R
R be a prime element.
Let
a  R
R be an element and let
(
a0,
a1,...,
ad)
be a
p-adic expansion of
a w.r.t.
p.
For every positive integer
k 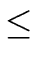 d
d + 1 we define
| a(k) = a0 + a1p + ... ak-1pk-1 |
(89) |
Then
a(k) is a
p-
adic approximation of
a at order
k,
that is
a(k)  a modpk. a modpk. |
(90) |
Proof.
Indeed, we have
| a - a(k) = akpk + ak+1pk+1 + ... + adpd = (ak + ak+1p + ... + adpd-k)pk |
|

Proposition 14
Let
R be a commutative ring with identity element
and let
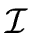
be an ideal of
R.
Let
a,
b  R
R be elements, let
k be a positive integer
and let

 R
R[
y] be a polynomial.
Then we have
a  b mod b mod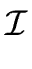 k k   (a) (a)   (b)mod (b)mod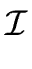 k k |
(91) |
That is, if
a is an
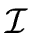
-adic approximation
of
b at order
k, then

(
a) is an
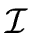
-adic approximation
of

(
b) at order
k.
Proof.
This is simply because of the ring-homomorphism between
R and
R/
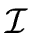
.



Next: Symbolic Newton Iteration
Up: Advanced Computer Algebra: From Newton
Previous: Division with remainder using Newton
Marc Moreno Maza
2004-04-27
![]() 0 holds.
This implies
0 holds.
This implies
![]() (p) >
(p) > ![]() (a0).
If a0 would have positive degree k w.r.t. p,
then, by the properties of a regular Euclidean size,
we would have
(a0).
If a0 would have positive degree k w.r.t. p,
then, by the properties of a regular Euclidean size,
we would have
![]() (a0)
(a0) ![]()
![]() (pk).
Since
(pk).
Since
![]() (pk)
(pk) ![]()
![]() (p) holds (by definition
of an Euclidean domain) we would have a contradiction
with
(p) holds (by definition
of an Euclidean domain) we would have a contradiction
with
![]() (p) >
(p) > ![]() (a0).
Therefore in any case we have
deg(a0, p) = 0.
(a0).
Therefore in any case we have
deg(a0, p) = 0.
![]() (a) <
(a) < ![]() (p).
Hence every quotient of a w.r.t. p is null.
(Otherwise we would have
(p).
Hence every quotient of a w.r.t. p is null.
(Otherwise we would have
![]() (p)
(p) ![]()
![]() (a)
by the properties of a regular Euclidean size.)
Since a = a0 and since a0 has degree 0 w.r.t. p,
the element a has degree 0 w.r.t. p and (a0)
is a p-adic expansion of a w.r.t. p.
Therefore the proposition is proved in the case
of the elements a which have quotient 0 w.r.t. p.
(a)
by the properties of a regular Euclidean size.)
Since a = a0 and since a0 has degree 0 w.r.t. p,
the element a has degree 0 w.r.t. p and (a0)
is a p-adic expansion of a w.r.t. p.
Therefore the proposition is proved in the case
of the elements a which have quotient 0 w.r.t. p.
![]() 0 and
0 and
![]() (q0) <
(q0) < ![]() (a) hold.
Then let
(q1, a1) be a couple quotient-remainder
given as in
Definition 7
when dividing q0 w.r.t. p.
If
q1
(a) hold.
Then let
(q1, a1) be a couple quotient-remainder
given as in
Definition 7
when dividing q0 w.r.t. p.
If
q1 ![]() 0 then we have
0 then we have
![]() (q1) <
(q1) < ![]() (q0)
and let
(q2, a2) be a couple quotient-remainder
given as in
Definition 7
when dividing q1 w.r.t. p.
Continuing in this manner we obtain a finite sequence
a0, a1,..., ad
(q0)
and let
(q2, a2) be a couple quotient-remainder
given as in
Definition 7
when dividing q1 w.r.t. p.
Continuing in this manner we obtain a finite sequence
a0, a1,..., ad ![]() R and a finite sequence
q0, q1,..., qd
R and a finite sequence
q0, q1,..., qd ![]() R such that we have
R such that we have
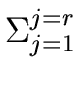
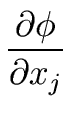 (
(