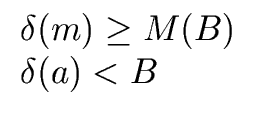

Next: Gcd Algorithms in [x1,..., xn]
Up: Advanced Computer Algebra: The resultant
Previous: A modular Gcd Algorithm in
We present now another generalization of
Algorithm 3:
the case of univariate polynomials over an Euclidean domain E
with an Euclidean size 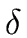 .
This idea appears in [KM99].
We need two assumptions for E.
.
This idea appears in [KM99].
We need two assumptions for E.
First we assume that we have access to the stream of unassociated primes
p1, p2, p3,..., such that
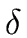 (p1) <
(p1) < 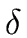 (p1p2) <
(p1p2) < 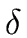 (p1p2p3) < ... .
Indeed the recovery of an element a in E from
a modm=p1 ... pn
requires sufficiently large m.
(p1p2p3) < ... .
Indeed the recovery of an element a in E from
a modm=p1 ... pn
requires sufficiently large m.
Secondly, we assume the avialability of a mapping
scs
from
E×E 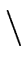 {0} to E, called a symmetric canonical simplifier,
such that we have the following properties.
{0} to E, called a symmetric canonical simplifier,
such that we have the following properties.
- Simplification.
- Any element a
 E must satisfy
a
E must satisfy
a 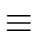 scs(a, m) for any
m
scs(a, m) for any
m  E
E 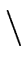 {0}. More formally:
{0}. More formally:
( a a 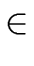 E)( E)( m m 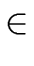 E E 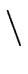 {0}) a {0}) a 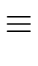 scs(a, m). scs(a, m). |
(116) |
- Canonicity.
- For any
m
 E
E 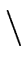 {0},
any two elements a, b
{0},
any two elements a, b  E equivalent modulo m
must satisfy
scs(a, m) = scs(b, m). More formally:
E equivalent modulo m
must satisfy
scs(a, m) = scs(b, m). More formally:
( a, b a, b 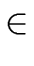 E)( E)( m m 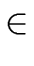 E E 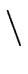 {0}) (a {0}) (a 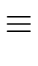 b) b) 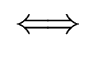 (scs(a, m) = scs(b, m)). (scs(a, m) = scs(b, m)). |
(117) |
- Recoverage = symmetry.
- All elements of a bounded degree are recovered
by the simplifier if the modulus is sufficiently large.
( B > 0)( B > 0)(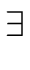 M M 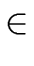 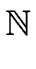 )( )( (a, m) (a, m) 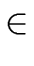 E×E E×E 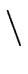 {0}) {0}) 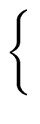 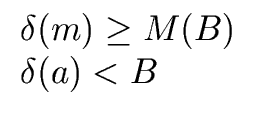  scs(a, m) = a. scs(a, m) = a. |
(118) |
Algorithm 5
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] $f,g \in ...
...n} $h$\ \\
\> \> $(m, g_m)$\ := $(m \, p, w)$\ \\
\end{tabbing}\end{minipage}}](img146.png)
See [KM99] for more details.


Next: Gcd Algorithms in [x1,..., xn]
Up: Advanced Computer Algebra: The resultant
Previous: A modular Gcd Algorithm in
Marc Moreno Maza
2004-04-27
![]() (p1) <
(p1) < ![]() (p1p2) <
(p1p2) < ![]() (p1p2p3) < ... .
Indeed the recovery of an element a in E from
a modm=p1 ... pn
requires sufficiently large m.
(p1p2p3) < ... .
Indeed the recovery of an element a in E from
a modm=p1 ... pn
requires sufficiently large m.
![]() {0} to E, called a symmetric canonical simplifier,
such that we have the following properties.
{0} to E, called a symmetric canonical simplifier,
such that we have the following properties.
 (scs(a, m) = scs(b, m)).
(scs(a, m) = scs(b, m)).