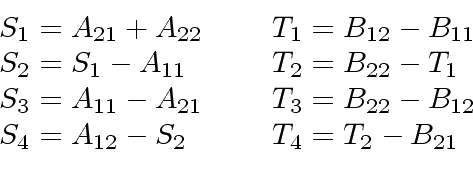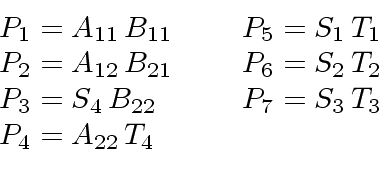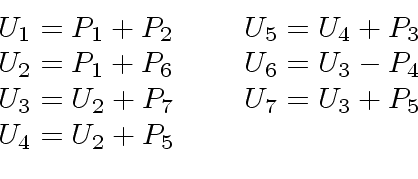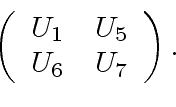Let
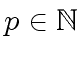 and
and 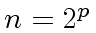 .
Let
.
Let 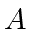 and
and 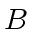 be two square matrices of order
be two square matrices of order 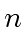 and with coefficients in
and with coefficients in
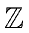 .
The classical algorithm for computing the matrix product
.
The classical algorithm for computing the matrix product 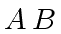 uses
uses
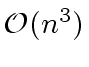 operations in
operations in
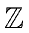 .
The Strassen algorithm provides the lower asymptotic upper bound
.
The Strassen algorithm provides the lower asymptotic upper bound
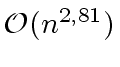 .
As for the Karatsuba algorithm, the trick relies on a smart use
of distributivity:
.
As for the Karatsuba algorithm, the trick relies on a smart use
of distributivity:
- If
 the matrices
the matrices 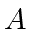 et
et 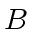 are of the form
are of the form 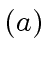 et
et 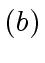 where
where
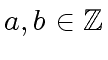 , such that
, such that 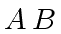 equals
equals 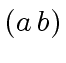 .
.
- If
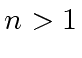 the matrices
the matrices 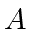 and
and 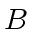 can be decomposed as
can be decomposed as
where 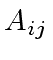 and
and 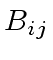 are square matrices
of order
are square matrices
of order 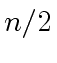 .
Them, one computes the following 8 sums.
.
Them, one computes the following 8 sums.
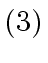
- Next, one computes the following 7 matrix products by recursive calls
to the algorithm.
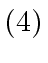
- Finally, one computes the following 7 sums:
and one returns:
Marc Moreno Maza
2008-03-18
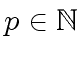 and
and 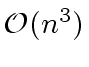 operations in
operations in
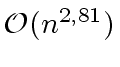 .
As for the Karatsuba algorithm, the trick relies on a smart use
of distributivity:
.
As for the Karatsuba algorithm, the trick relies on a smart use
of distributivity:
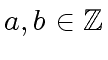 , such that
, such that 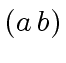 .
.
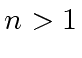 the matrices
the matrices 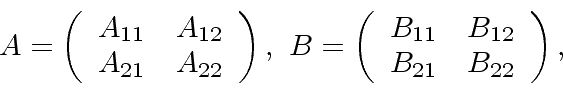
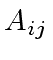 and
and 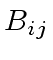 are square matrices
of order
are square matrices
of order 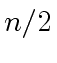 .
Them, one computes the following 8 sums.
.
Them, one computes the following 8 sums.