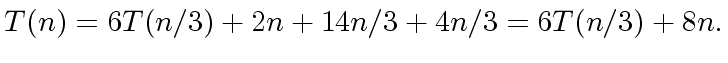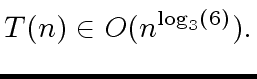
- Write
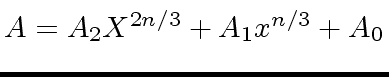 and
and
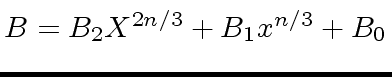 where
where
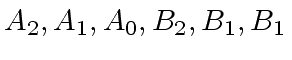 are polynomials
of degree less than
are polynomials
of degree less than 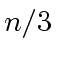 .
We want to compute
.
We want to compute 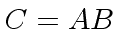 . We have
. We have
with
Note that each of the polynomials
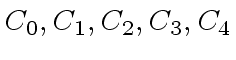 has
degree less than
has
degree less than  .
Computing the coefficients
.
Computing the coefficients
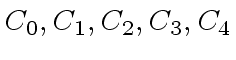 requires
requires
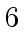 additions in degree less than
additions in degree less than 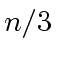 .
.
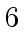 multiplications in degree less than
multiplications in degree less than 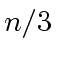 .
.
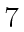 additions in degree less than
additions in degree less than  .
.
Once the coefficients
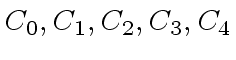 have been computed
the true coefficients of
have been computed
the true coefficients of 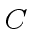 are not known yet.
For intsance, both
are not known yet.
For intsance, both
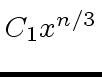 and
and 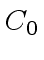 contain terms
in degree
contain terms
in degree 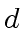 for
for
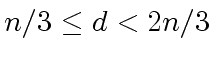 .
In fact, we need
.
In fact, we need 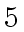 additions in degree less than
additions in degree less than 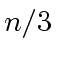 in order to complete the job.
in order to complete the job.
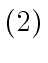
- Let
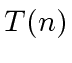 be the number of operations on the coefficients
required to compute
be the number of operations on the coefficients
required to compute 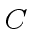 from
from 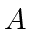 and
and 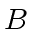 . We have
. We have
Using the appropiate formula from [TCS02].
we obtain
Marc Moreno Maza
2008-03-18
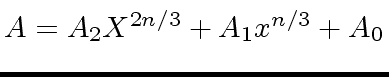 and
and
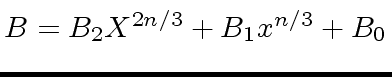 where
where
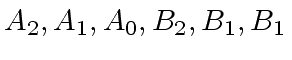 are polynomials
of degree less than
are polynomials
of degree less than 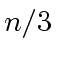 .
We want to compute
.
We want to compute 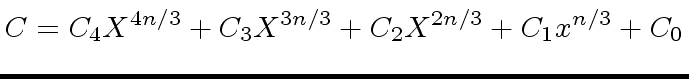
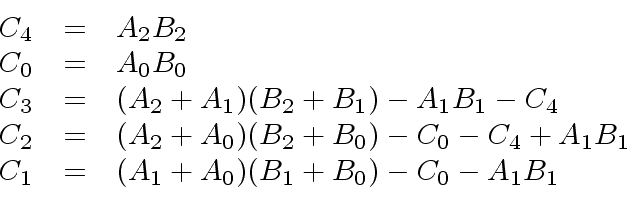
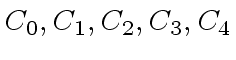 has
degree less than
has
degree less than  .
Computing the coefficients
.
Computing the coefficients
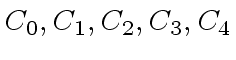 requires
requires
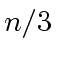 .
.
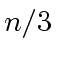 .
.
 .
.
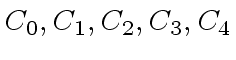 have been computed
the true coefficients of
have been computed
the true coefficients of 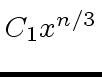 and
and 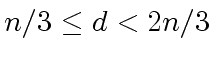 .
In fact, we need
.
In fact, we need 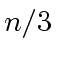 in order to complete the job.
in order to complete the job.
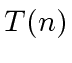 be the number of operations on the coefficients
required to compute
be the number of operations on the coefficients
required to compute