Next: Questions Up: Exercise 3 Previous: Exercise 3
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) be two polynomials with respective degrees
be two polynomials with respective degrees
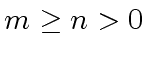 .
We assume that the leading coefficient
.
We assume that the leading coefficient
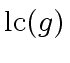 of
of 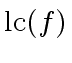 of
of ![$ q \in {\mbox{${\mathbb{Z}}$}}[x]$](img108.png) such that
such that 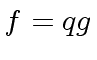 holds.
Moreover, if
holds.
Moreover, if
Another obvious necessary condition (for ![]() to divide
to divide ![]() exactly)
is that the trailing coefficient
of
exactly)
is that the trailing coefficient
of ![]() (that is the coefficient of
(that is the coefficient of ![]() of its non-zero term with smallest degree)
divides that of
of its non-zero term with smallest degree)
divides that of ![]() .
So, we assume that this condition holds too.
.
So, we assume that this condition holds too.
If ![]() and
and ![]() are random enough the probability for
are random enough the probability for ![]() to divide
to divide ![]() exactly is clearly low.
So we aim at designing a modular method that will take advantage of this remark.
exactly is clearly low.
So we aim at designing a modular method that will take advantage of this remark.
Marc Moreno Maza