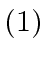
- Assume that
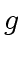 divides
divides 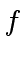 and let
and let 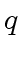 be the quotient.
The degree of
be the quotient.
The degree of 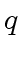 is
is 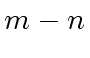 .
Viewing
.
Viewing 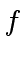 ,
, 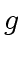 and
and 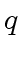 as polynomials in
as polynomials in
![$ {\mbox{${\mathbb{Q}}$}}[x]$](img115.png) one can use Lagrange interpolation to construct
one can use Lagrange interpolation to construct 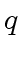 from its values at
from its values at
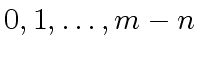 .
This idea leads to the following algorithm.
.
This idea leads to the following algorithm.
- Let
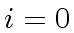 .
.
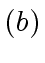
- While
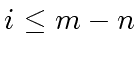 repeat
repeat
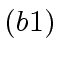
- Compute
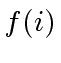 and
and 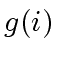 .
.
- If
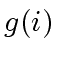 does not divide
does not divide 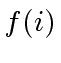 in
in
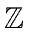 then return
``g does not divide f'' otherwise define
then return
``g does not divide f'' otherwise define
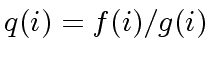 .
.
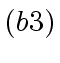
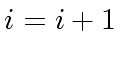 .
.

- Interpolate
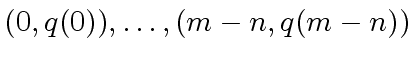 in order to get
in order to get 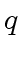 and return it.
and return it.
- Assume again that
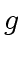 divides
divides 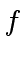 and let
and let 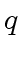 be the quotient.
This means that
be the quotient.
This means that 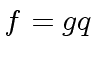 in
in
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) .
Let
.
Let 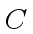 be an upper for the absolute value of a coefficient in
be an upper for the absolute value of a coefficient in 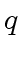 .
(Actually, one can adapt Exercise 1 in order to obtain such a bound).
Let
.
(Actually, one can adapt Exercise 1 in order to obtain such a bound).
Let 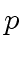 be a prime number.
Then, we have
be a prime number.
Then, we have
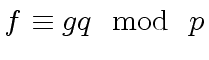 .
This idea leads to the following algorithm.
.
This idea leads to the following algorithm.
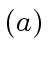
- Let
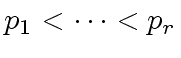 be machine-word-size
odd primes such that their product
be machine-word-size
odd primes such that their product 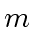 exceeds
exceeds 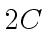
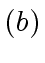
- For all
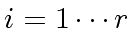 repeat:
repeat:
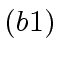
- compute the images
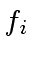 and
and 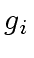 of
of 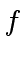 and
and 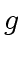 in
in
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png) ,
,
- compute the quotient
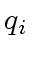 and remainder
and remainder 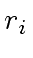 in the division of
in the division of 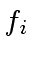 by
by 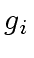 in
in
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png) ,
,
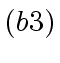
- if
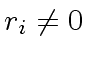 then return
``g does not divide f''
then return
``g does not divide f''

- Use the Chinese Remainder Algorithm coefficient-wise in order
to construct a polynomial
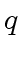 from
from
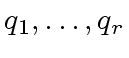 .
.
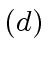
- If
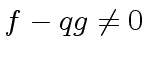 then return
``g does not divide f'' otherwise return
then return
``g does not divide f'' otherwise return 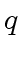 .
.
The checking statement 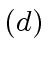 can be avoided but this requires
additional material outside of the scope of this course.
can be avoided but this requires
additional material outside of the scope of this course.
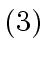
- The second approach is probably better since it is
a modular method relying on modular computations over machine-word-size
finite fields.
But, of course, the bound
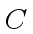 has to be sharp.
has to be sharp.
Marc Moreno Maza
2008-03-18
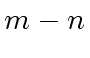 .
Viewing
.
Viewing ![$ {\mbox{${\mathbb{Q}}$}}[x]$](img115.png) one can use Lagrange interpolation to construct
one can use Lagrange interpolation to construct 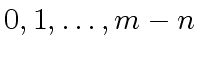 .
This idea leads to the following algorithm.
.
This idea leads to the following algorithm.
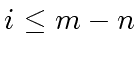 repeat
repeat
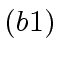
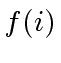 and
and 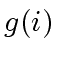 .
.
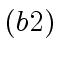
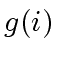 does not divide
does not divide 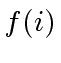 in
in
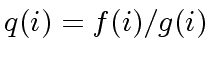 .
.
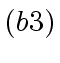
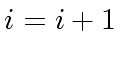 .
.
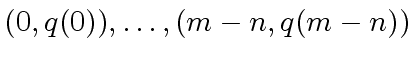 in order to get
in order to get 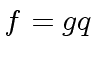 in
in
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) .
Let
.
Let 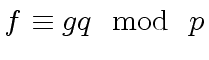 .
This idea leads to the following algorithm.
.
This idea leads to the following algorithm.
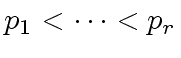 be machine-word-size
odd primes such that their product
be machine-word-size
odd primes such that their product 
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png) ,
,
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png) ,
,
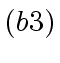
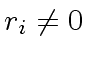 then return
``g does not divide f''
then return
``g does not divide f''
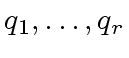 .
.
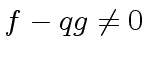 then return
``g does not divide f'' otherwise return
then return
``g does not divide f'' otherwise return