Next: Questions Up: Exercise 4 Previous: Exercise 4
![$ {\mbox{${\mathbb{K}}$}}[x_1]$](img135.png) .
Let
.
Let  be an upper bound for the number of operations
in
be an upper bound for the number of operations
in
![$ {\mbox{${\mathbb{K}}$}}[x_1]$](img135.png) with degree at most
with degree at most
We would like to derive a fast algorithm for multiplying
bivariate polynomials in
![$ {\mbox{${\mathbb{K}}$}}[x_1,x_2]$](img138.png) .
To do so, we consider the following transformation.
.
To do so, we consider the following transformation.
Let
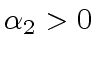 be a positive integer.
Given a bivariate polynomial
be a positive integer.
Given a bivariate polynomial ![]() we replace every monomial
we replace every monomial
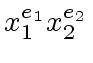 of
of ![]() by
by
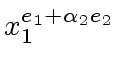 obtaining a univariate polynomial
obtaining a univariate polynomial ![]() .
Let
.
Let ![]() be the degree of
be the degree of ![]() w.r.t.
w.r.t. ![]() and
and ![]() its degree w.r.t.
its degree w.r.t. ![]() ,
,
Marc Moreno Maza