Next: Hints Up: Exercise 4 Previous: Questions
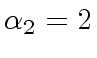 , we have
, we have
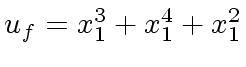 and with
and with
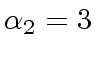 , we have
, we have
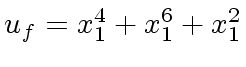 .
.
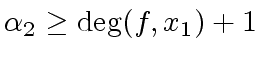 .
.
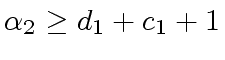 .
.
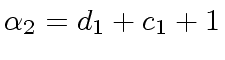 compute
compute
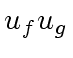 in
in
![$ {\mbox{${\mathbb{K}}$}}[x_1]$](img135.png) ,
then its (unique) preimage
,
then its (unique) preimage 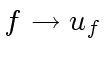 ,
,
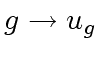 ,
and
,
and
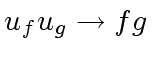 have a linear cost
in the number of terms of their results.
So the dominant cost is the computation of the product
have a linear cost
in the number of terms of their results.
So the dominant cost is the computation of the product 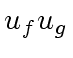 which is clearly in
which is clearly in
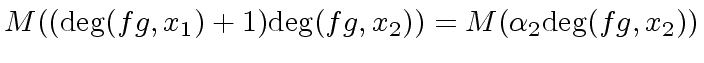 operations in
operations in
Marc Moreno Maza