We make a preliminary observation.
Let 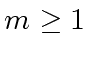 be an odd integer such that we have
be an odd integer such that we have
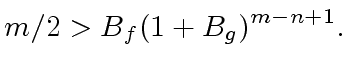 |
(10) |
Note that this implies
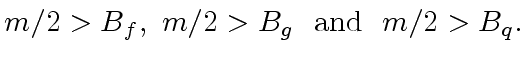 |
(11) |
We represent the elements of
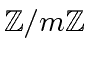 with the symmetric range
with the symmetric range
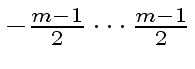 .
Let
.
Let 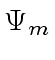 be the corresponding canonical ring homomorphism
from
be the corresponding canonical ring homomorphism
from
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) to
to
![$ {\mbox{${\mathbb{Z}}$}}/m{\mbox{${\mathbb{Z}}$}}[x]$](img39.png) .
In
.
In
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) we have:
we have:
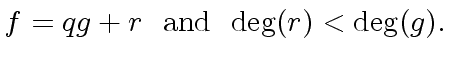 |
(12) |
This implies the following in
![$ {\mbox{${\mathbb{Z}}$}}/m{\mbox{${\mathbb{Z}}$}}[x]$](img39.png) :
:
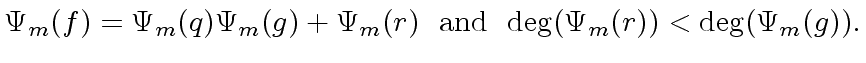 |
(13) |
Observe that we have:
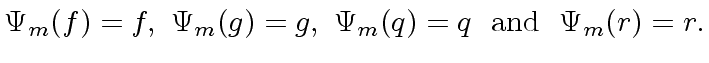 |
(14) |
We shall describe now how to compute
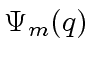 and
and
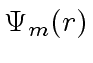 ,
and thus
,
and thus 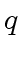 and
and 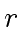 .
.
Consider
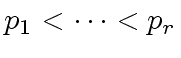 odd primes such that their product
odd primes such that their product 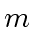 satisfies (10).
For all
satisfies (10).
For all
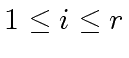 , let
, let 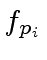 ,
, 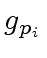 ,
, 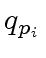 and
and 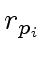 be the respective images of
be the respective images of 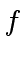 ,
, 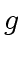 ,
, 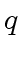 and
and 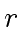 in
in
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png) .
Thus, for all
.
Thus, for all
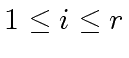 , we have in
, we have in
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png)
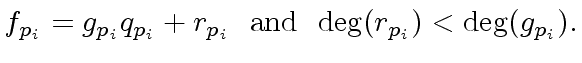 |
(15) |
By virtue of the uniqueness of the division by a monic polynomial,
this implies that for all
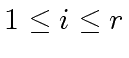 , the couple
, the couple
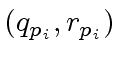 is the couple quotient-remainder in the division of
is the couple quotient-remainder in the division of 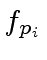 by
by 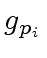 .
Applying coefficient-wise the Chinese Remaindering Algorithm
(see course notes) we construct polynomials
.
Applying coefficient-wise the Chinese Remaindering Algorithm
(see course notes) we construct polynomials
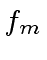 ,
, 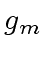 ,
, 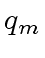 and
and 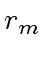 in
in
![$ {\mbox{${\mathbb{Z}}$}}/m{\mbox{${\mathbb{Z}}$}}[x]$](img39.png) such that
such that
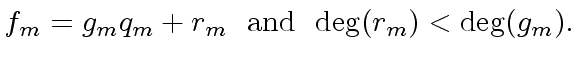 |
(16) |
Moreover, the Chinese Remaindering Theorem tells us that we have:
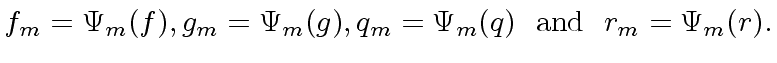 |
(17) |
Using the preliminary remark, we conclude that 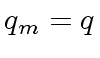 and
and 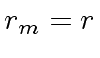 .
This approach is interesting when fast division is available
in each
.
This approach is interesting when fast division is available
in each
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png) .
.
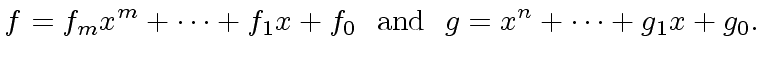
![]() has degree
has degree 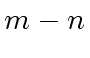 , so we define:
, so we define:
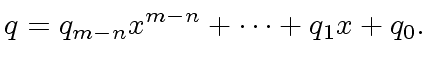
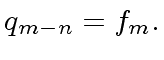
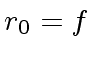 be the ``initial'' remainder
and let
be the ``initial'' remainder
and let
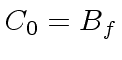 be the largest absolute value of a coefficient in
be the largest absolute value of a coefficient in 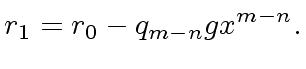
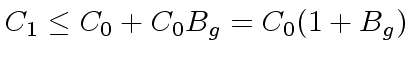
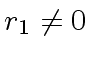 , then the next intermediate remainder
, then the next intermediate remainder 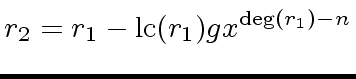
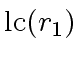 is the leading coefficient of
is the leading coefficient of 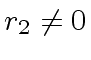 , then
, then 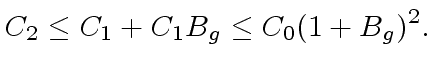
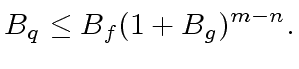
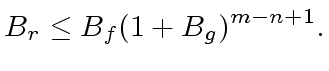
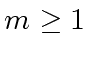 be an odd integer such that we have
be an odd integer such that we have
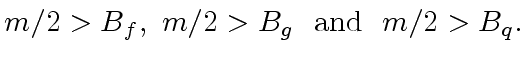
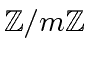 with the symmetric range
with the symmetric range
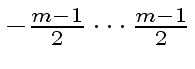 .
Let
.
Let 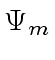 be the corresponding canonical ring homomorphism
from
be the corresponding canonical ring homomorphism
from
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) to
to
![$ {\mbox{${\mathbb{Z}}$}}/m{\mbox{${\mathbb{Z}}$}}[x]$](img39.png) .
In
.
In
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img3.png) we have:
we have:
![$ {\mbox{${\mathbb{Z}}$}}/m{\mbox{${\mathbb{Z}}$}}[x]$](img39.png) :
:
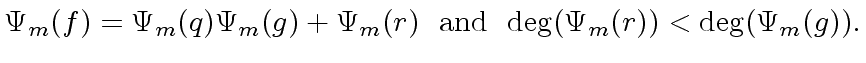
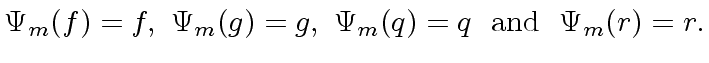
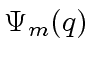 and
and
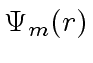 ,
and thus
,
and thus 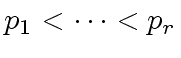 odd primes such that their product
odd primes such that their product ![]() satisfies (10).
For all
satisfies (10).
For all
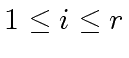 , let
, let ![]() ,
, ![]() ,
, ![]() and
and ![]() be the respective images of
be the respective images of ![]() ,
, ![]() ,
, ![]() and
and ![]() in
in
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png) .
Thus, for all
.
Thus, for all
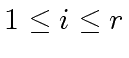 , we have in
, we have in
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png)
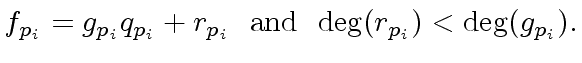
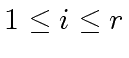 , the couple
, the couple
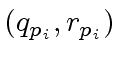 is the couple quotient-remainder in the division of
is the couple quotient-remainder in the division of ![$ {\mbox{${\mathbb{Z}}$}}/m{\mbox{${\mathbb{Z}}$}}[x]$](img39.png) such that
such that
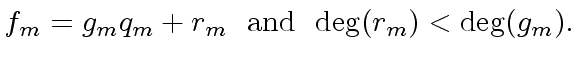
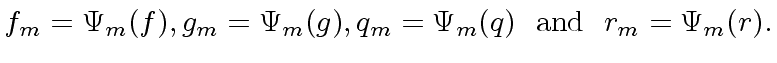
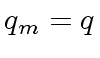 and
and 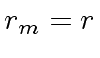 .
This approach is interesting when fast division is available
in each
.
This approach is interesting when fast division is available
in each
![$ {\mbox{${\mathbb{Z}}$}}/p_i{\mbox{${\mathbb{Z}}$}}[x]$](img52.png) .
.
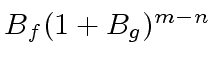 is an upper bound for (the absolute value of
a coefficient in) the quotient
is an upper bound for (the absolute value of
a coefficient in) the quotient
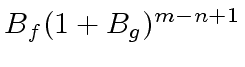 ;
alternatively, we can
;
alternatively, we can
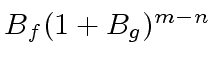 ,
,
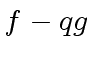 .
.