Next: The Euclidean Algorithm Up: The Euclidean Algorithm Previous: The Euclidean Algorithm
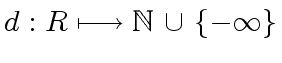 is an Euclidean domain if the following two conditions hold
is an Euclidean domain if the following two conditions hold
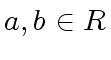 with
with 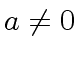 and
and 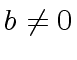 we have
we have
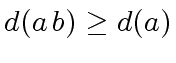 ,
,
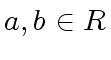 with
with 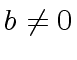 there exist
there exist 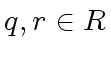 such that
such that
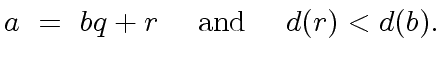 |
(1) |
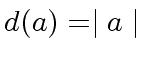 for
for
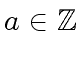 .
Here the quotient
.
Here the quotient 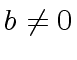 ) can be made unique by requiring
) can be made unique by requiring 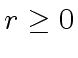 (hence we have
(hence we have
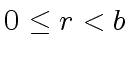 ).
).
![$ R = {\bf k}[x]$](img19.png) where
where 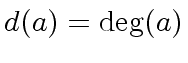 the degree of
the degree of 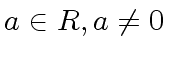 and
and
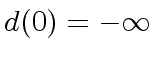 .
Uniqueness of the quotient and the remainder is easy to show
in that case. Indeed
.
Uniqueness of the quotient and the remainder is easy to show
in that case. Indeed
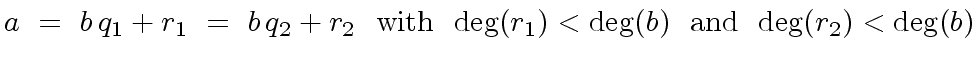 |
(2) |
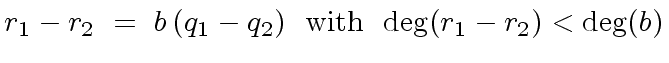 |
(3) |
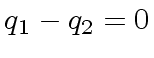 and thus
and thus
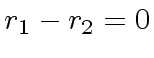 .
.
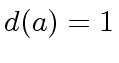 for
for
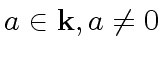 and
and 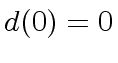 .
In this case the quotient
.
In this case the quotient 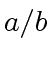 and 0
respectively.
and 0
respectively.
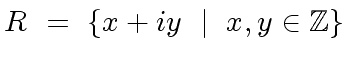 |
(4) |
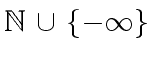 the norm of an element.
Hence
the norm of an element.
Hence
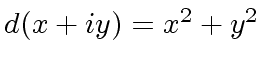 with
with
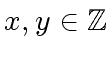 .
It is easy to check that for every
.
It is easy to check that for every 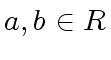 with
with
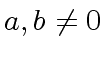 we have
we have
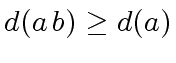 .
Indeed for
.
Indeed for
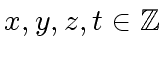 we have
we have
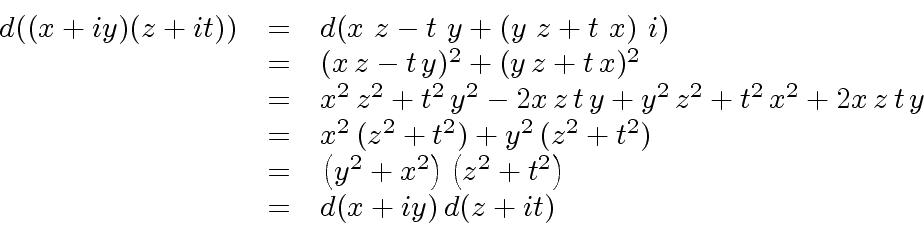 |
(5) |
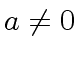 we have
we have
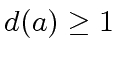 .
Therefore we have proved that
.
Therefore we have proved that
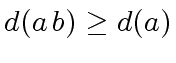 holds
for every
holds
for every 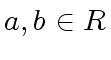 with
with
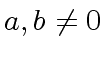 .
Now given
.
Now given 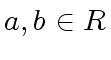 with
with 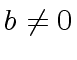 we are looking for
a quotient and a remainder of
we are looking for
a quotient and a remainder of 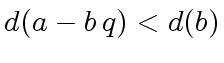 .
Such a
.
Such a 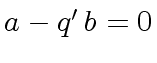 that is
that is
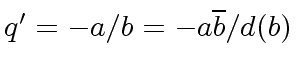 where
where
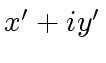 with
with
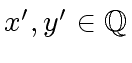 .
Let
.
Let
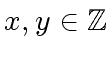 be such that
be such that
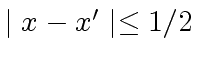 and
and
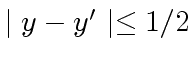 .
Then
.
Then
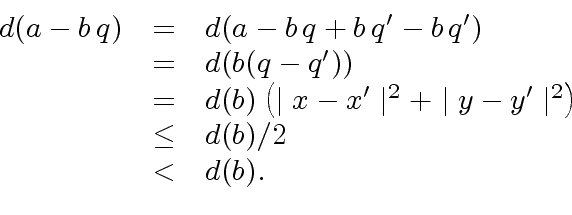 |
(6) |
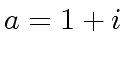 and
and
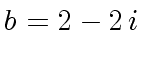 we have
we have
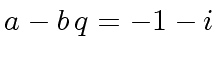 with
with 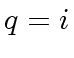 and
and
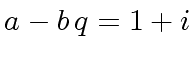 with
with 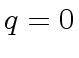 .
In both cases
.
In both cases
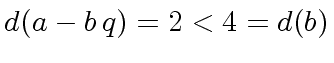 .
Finally this shows that a quotient and a remainder of
.
Finally this shows that a quotient and a remainder of Marc Moreno Maza