In order to analyze Algorithms 2 and 3
we introduce the following matrices
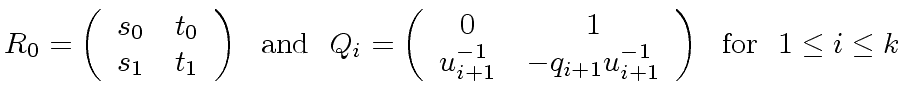 |
(12) |
with coefficients in  .
Then, we define
.
Then, we define
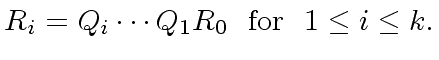 |
(13) |
The following proposition collects some invariants of the
Extended Euclidean Algorithm.
Proposition 1
With the convention that
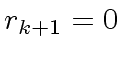 and
and
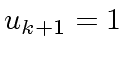 ,
for
,
for
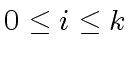 we have
we have
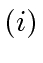
-
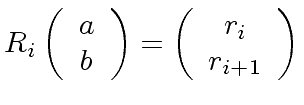 ,
,
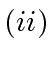
-
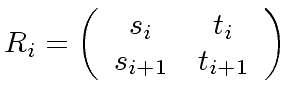 ,
,
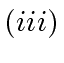
-
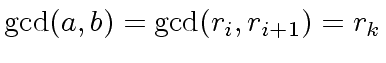 ,
,
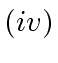
-
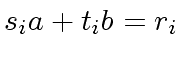 and
and
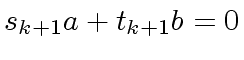 ,
,
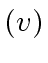
-
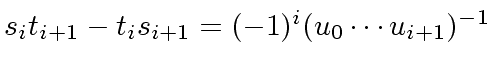 ,
,
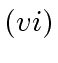
-
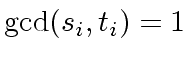 ,
,
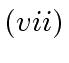
-
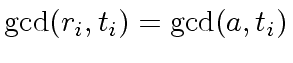 ,
,
- the matrices
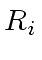 and
and 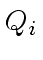 are invertible;
are invertible;
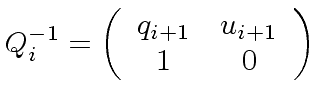 and
and
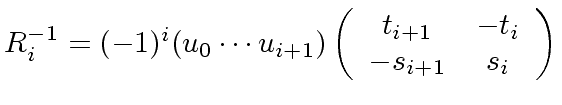 ,
,
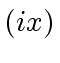
-
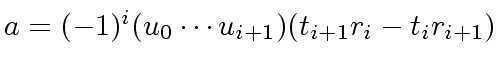 ,
,
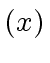
-
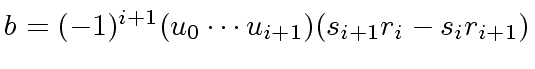 .
.
Proof.
We prove
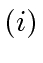
and
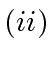
by induction on
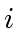
.
The case
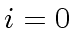
follows immediately from the definitions
of
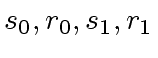
and
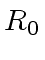
.
We assume that
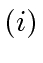
and
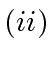
hold for
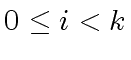
.
By induction hypothesis, we have
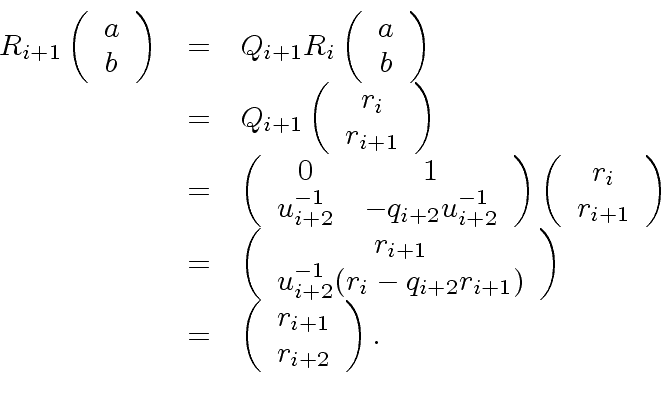 |
(14) |
Similarly, we have
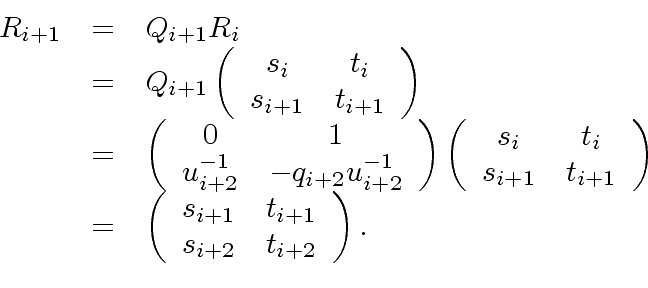 |
(15) |
Property
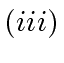
follows from our study of Algorithm
1.
Claim
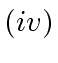
follows
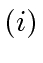
and
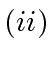
.
Taking the determinant of each side of
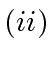
we prove
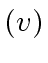
as follows:
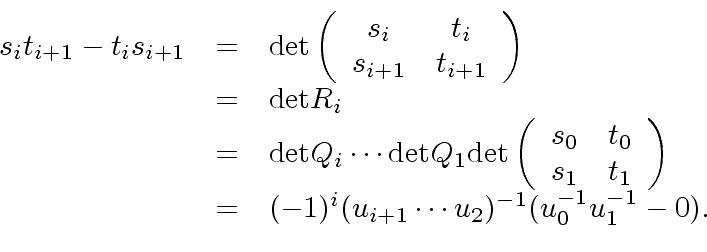 |
(16) |
Now, we prove
.
If
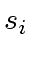
and
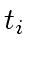
would have a non-invertible common factor, then it would
divide
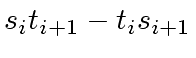
.
This contradicts
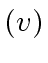
and proves
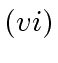
.
We prove
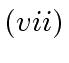
.
Let
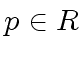
be a divisor of
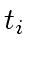
.
If
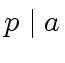
, then
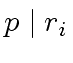
holds since we have
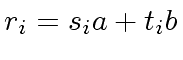
from
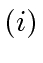
.
If
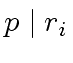
, then
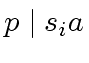
and, thus,
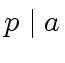
since
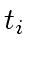
and
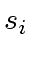
are relatively prime, from
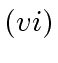
.
Therefore,
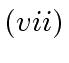
holds.
We prove
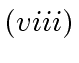
.
From
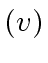
, we deduce that
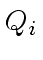
is invertible.
Then, the invertibility of
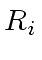
follows easily from that of
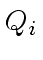
.
It is routine to check that the proposed inverses are correct.
Finally, claims
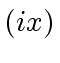
and
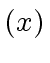
are derived from
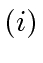
by multiplying each side with the inverse of
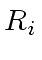
given in
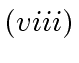
.

In the case
![$ R = {\bf k}[x]$](img19.png) where
where 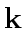 is a field,
the following Proposition 2
shows that the degrees of
the Bézout coefficients of the
Extended Euclidean Algorithm grow linearly
whereas Proposition 3
shows that Bézout coefficients are essentially unique,
provided that their degrees are small enough.
is a field,
the following Proposition 2
shows that the degrees of
the Bézout coefficients of the
Extended Euclidean Algorithm grow linearly
whereas Proposition 3
shows that Bézout coefficients are essentially unique,
provided that their degrees are small enough.
Proof.
We only prove the first equality since the second one can be verified
in a similar way.
In fact, we prove this first equality together with
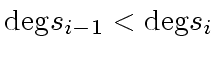 |
(19) |
by induction on
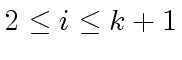
.
For
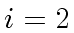
, the first equality holds since we have
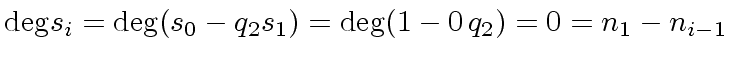 |
(20) |
and the inequality holds since we have
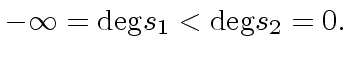 |
(21) |
Now we consider
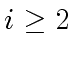
and we assume that both properties
hold for
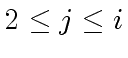
.
Then, by induction hypothesis, we have
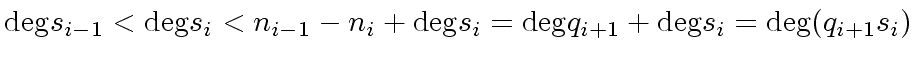 |
(22) |
which implies
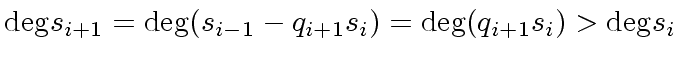 |
(23) |
and
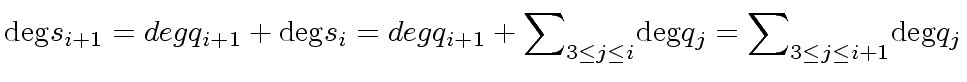 |
(24) |
where we used the induction hypothesis also.

Proof.
First, we observe that the index
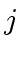
exists and is unique. Indeed,
we have
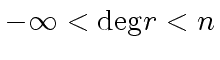
and,
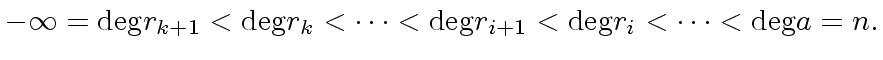 |
(28) |
Second, we claim that
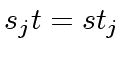 |
(29) |
holds.
Suppose that the claim is false and consider the following linear
system over
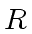
with
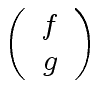
as unknown:
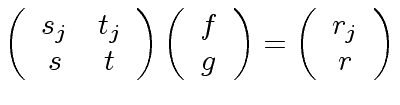 |
(30) |
Since the matrix of this linear system is non-singular, we can solve for
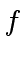
over the field of fractions of
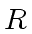
.
Moreover, we know that
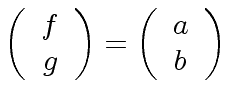
is the solution.
Hence, using Cramer's rule we obtain:
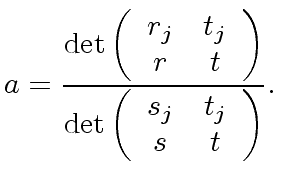 |
(31) |
The degree of the left hand side is
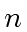
while the degree of the right hand side is equal or less than:
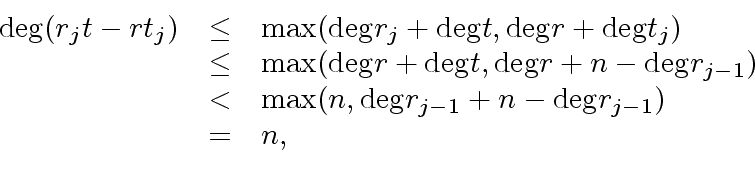 |
(32) |
by virtue of the definition of
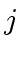
, Relation (
25) and
Proposition
2.
This leads to a contradiction.
Hence, we have
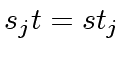
.
This implies that
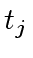
divides
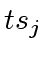
.
Since
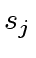
and
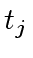
are relatively prime (Point
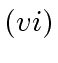
of Proposition
1) we deduce that
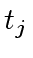
divides
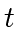
.
So let
![$ {\alpha} \in {\bf k}[x]$](img158.png)
such that
we have
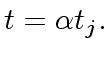 |
(33) |
Hence we obtain
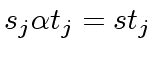
.
Since
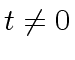
holds, we have
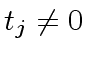
, leading to
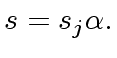 |
(34) |
Finally, plugging Equation (
33) and Equation (
34)
in Equation (
25), we obtain
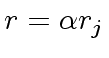
, as claimed.

Proposition 4
Let
![$ a, b \in {\bf k}[x]$](img181.png) where
where 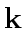 is a field.
Assume
is a field.
Assume
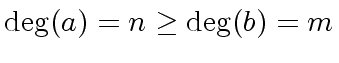 .
.
- Algorithm 3 requires at most
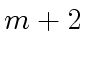 inversions and
inversions and
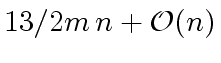 additions
and multiplications in
additions
and multiplications in 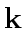 .
.
- If we do not compute the coefficients
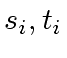 then
Algorithm 3 requires at most
then
Algorithm 3 requires at most
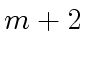 inversions and
inversions and
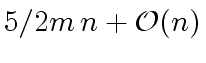 additions
and multiplications in
additions
and multiplications in 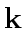 .
.
Proof.
See Theorem 3.11 in [
GG99].

Proposition 5
Let
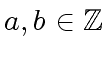 be multi-precision integers written with
be multi-precision integers written with
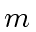 and
and 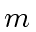 words.
Algorithm 3 can be performed in
words.
Algorithm 3 can be performed in
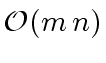 word operations.
word operations.
Proof.
See Theorem 3.13 in [
GG99].

Marc Moreno Maza
2008-01-07
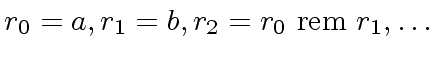 ,
,
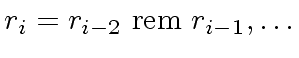 ,
,
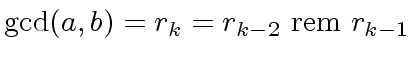 be as in Algorithm 1.
For
be as in Algorithm 1.
For
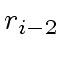 w.r.t.
w.r.t. 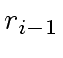 that is
that is
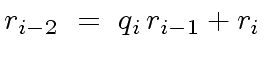
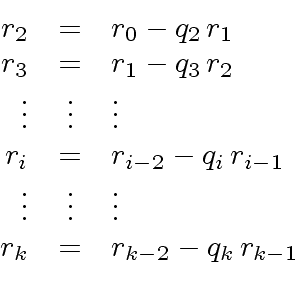
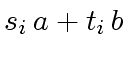 .
Indeed we have
.
Indeed we have
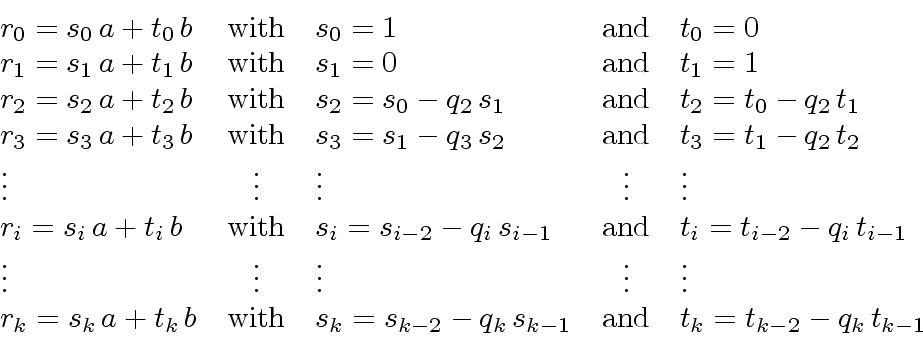
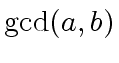 .
In order to compute a gcd together with its Bézout coefficients
Algorithm 1 needs to be transformed as follows.
The resulting algorithm (Algorithm 2)
is called the Extended Euclidean Algorithm.
Finally Algorithm 3 shows how to compute
the gcd together with its Bézout coefficients.
.
In order to compute a gcd together with its Bézout coefficients
Algorithm 1 needs to be transformed as follows.
The resulting algorithm (Algorithm 2)
is called the Extended Euclidean Algorithm.
Finally Algorithm 3 shows how to compute
the gcd together with its Bézout coefficients.
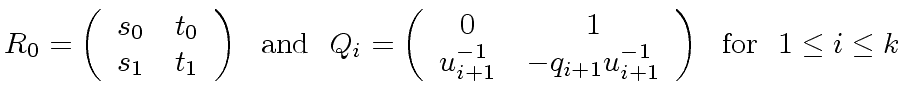
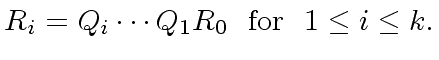
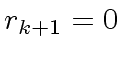 and
and
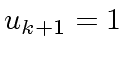 ,
for
,
for
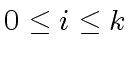 we have
we have
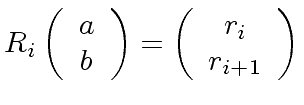 ,
,
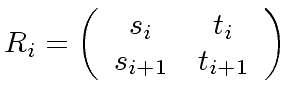 ,
,
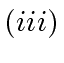
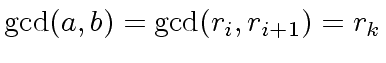 ,
,
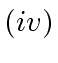
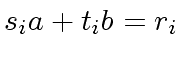 and
and
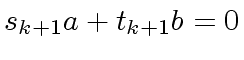 ,
,
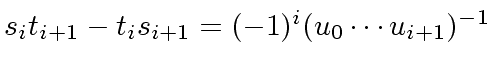 ,
,
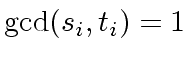 ,
,
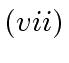
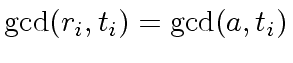 ,
,
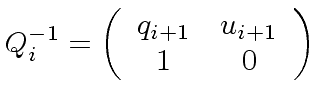 and
and
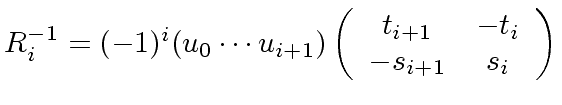 ,
,
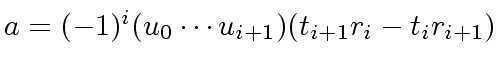 ,
,
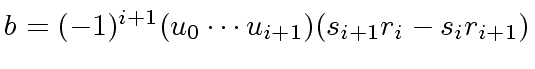 .
.
 by induction on
by induction on 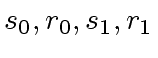 and
and  hold for
hold for
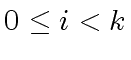 .
By induction hypothesis, we have
.
By induction hypothesis, we have
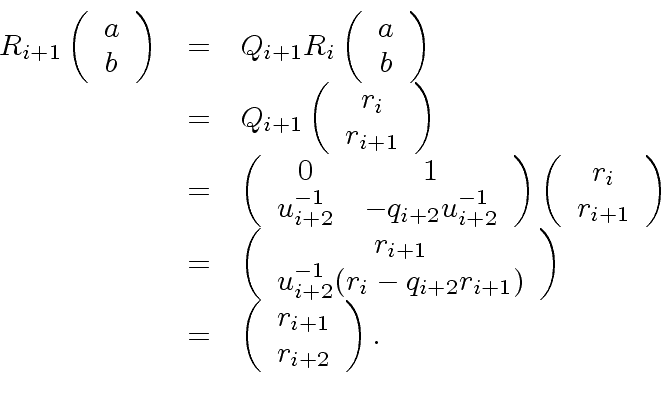
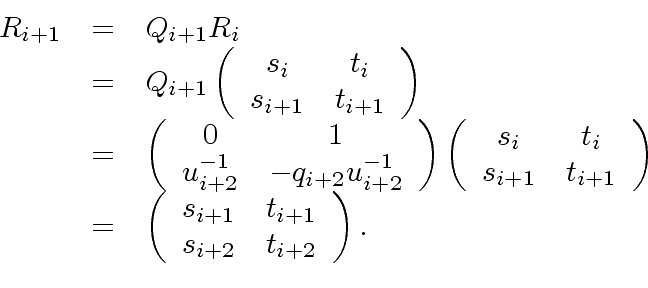
 follows from our study of Algorithm 1.
Claim
follows from our study of Algorithm 1.
Claim 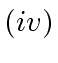 follows
follows 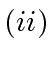 .
Taking the determinant of each side of
.
Taking the determinant of each side of 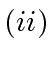 we prove
we prove 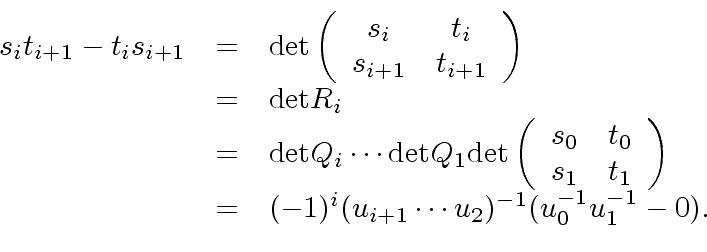
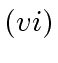 .
If
.
If 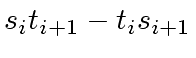 .
This contradicts
.
This contradicts 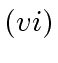 .
We prove
.
We prove 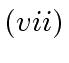 .
Let
.
Let 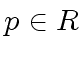 be a divisor of
be a divisor of 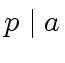 , then
, then
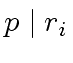 holds since we have
holds since we have
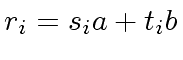 from
from 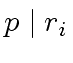 , then
, then
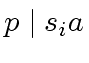 and, thus,
and, thus, 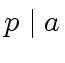 since
since
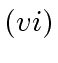 .
Therefore,
.
Therefore, 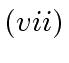 holds.
We prove
holds.
We prove 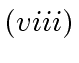 .
From
.
From 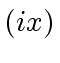 and
and 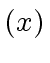 are derived from
are derived from  .
.
![$ R = {\bf k}[x]$](img19.png) where
where ![]() is a field,
the following Proposition 2
shows that the degrees of
the Bézout coefficients of the
Extended Euclidean Algorithm grow linearly
whereas Proposition 3
shows that Bézout coefficients are essentially unique,
provided that their degrees are small enough.
is a field,
the following Proposition 2
shows that the degrees of
the Bézout coefficients of the
Extended Euclidean Algorithm grow linearly
whereas Proposition 3
shows that Bézout coefficients are essentially unique,
provided that their degrees are small enough.
![$ R = {\bf k}[x]$](img19.png) where
where 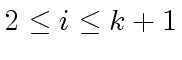 , we have
, we have
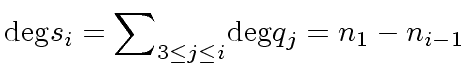
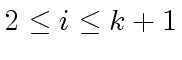 , we have
, we have
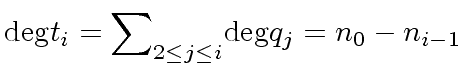
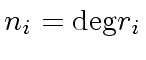 for
for
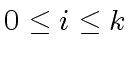 .
.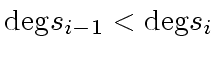
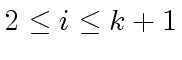 .
For
.
For 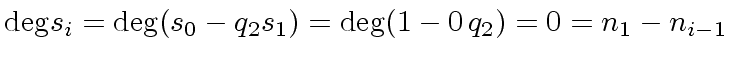
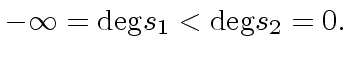
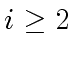 and we assume that both properties
hold for
and we assume that both properties
hold for
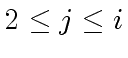 .
Then, by induction hypothesis, we have
.
Then, by induction hypothesis, we have
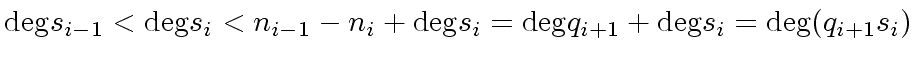
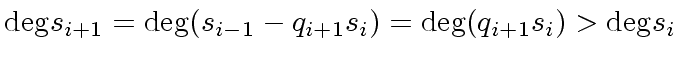
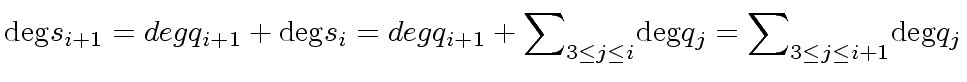
![$ R = {\bf k}[x]$](img19.png) where
where 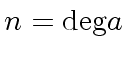 .
Let
.
Let
![$ r, s, t \in {\bf k}[x]$](img153.png) , with
, with 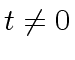 , be polynomials such that
, be polynomials such that
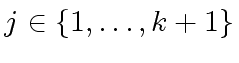 be such that
be such that
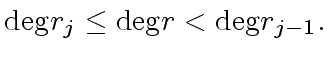
![$ {\alpha} \in {\bf k}[x]$](img158.png) such that
we have
such that
we have
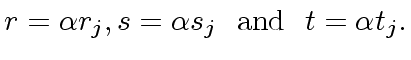
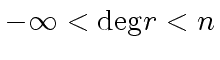 and,
and,
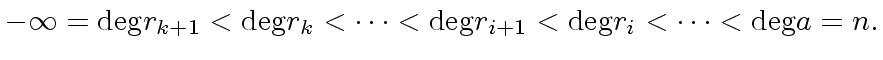
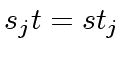
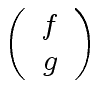 as unknown:
as unknown:
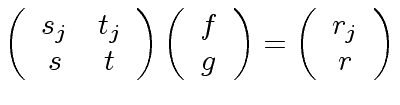
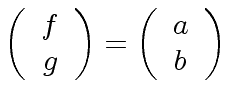 is the solution.
Hence, using Cramer's rule we obtain:
is the solution.
Hence, using Cramer's rule we obtain:
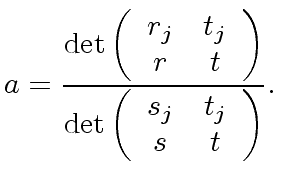
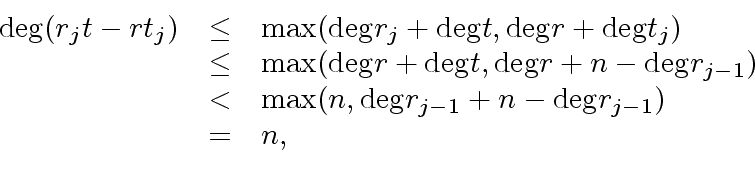
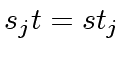 .
This implies that
.
This implies that  of Proposition 1) we deduce that
of Proposition 1) we deduce that
![$ {\alpha} \in {\bf k}[x]$](img158.png) such that
we have
such that
we have
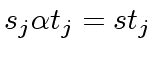 .
Since
.
Since 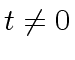 holds, we have
holds, we have
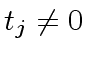 , leading to
, leading to
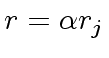 , as claimed.
, as claimed.
![$ a, b \in {\bf k}[x]$](img181.png) where
where 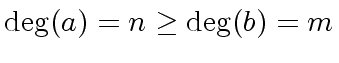 .
.
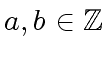 be multi-precision integers written with
be multi-precision integers written with
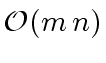 word operations.
word operations.