Next: The quotient as a modular Up: Division with remainder using Newton Previous: Division with remainder using Newton
![$ R[x]$](img5.png) with respective degrees
with respective degrees
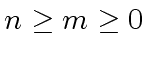 and the leading
coefficient of
and the leading
coefficient of 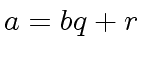 and
and
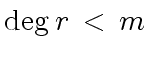 .
The polynomials
.
The polynomials 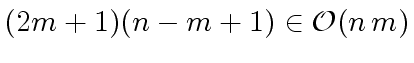 operations in
operations in
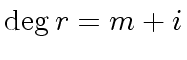 holds at the begining of the loop.
Observe that
holds at the begining of the loop.
Observe that 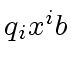 have the same leading coefficient.
Since
have the same leading coefficient.
Since
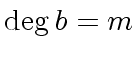 , computing the reductum of
, computing the reductum of 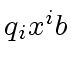 requires
requires 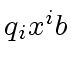 to that of
to that of 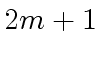 operations in
operations in 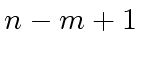 .
Therefore Algorithm 1
requires
.
Therefore Algorithm 1
requires
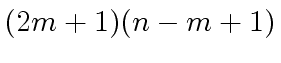 .
.
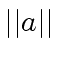 ,
,
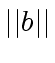 and
and
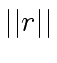 be the max-norm of
be the max-norm of 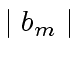 be the absolute value (over
be the absolute value (over
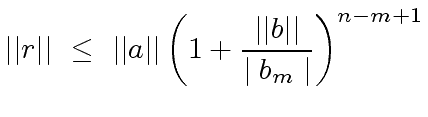 |
(1) |
Marc Moreno Maza