Next: Primitive roots of unity Up: Foundations of Computer Algebra: Fast Previous: Foundations of Computer Algebra: Fast
In the whole section we consider a commutative ring ![]() with units.
Let us consider two univariate polynomials
with units.
Let us consider two univariate polynomials
![$ f,g \in R[x]$](img5.png) of degree less than
of degree less than ![]() . Then their product has degree less than
. Then their product has degree less than 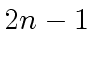 .
Assume that we are given a finite subset
.
Assume that we are given a finite subset
![]() of
of ![]() with
with
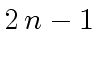 elements such that
elements such that
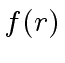 and
and 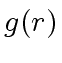 are known for every
are known for every 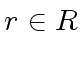 .
Then the values
.
Then the values
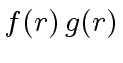 define the polynomial
define the polynomial ![]() completely.
Indeed, by Lagrange interpolation we construct the polynomial
completely.
Indeed, by Lagrange interpolation we construct the polynomial
![]() (which has at most
(which has at most 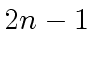 coefficients) from the
coefficients) from the
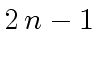 values
values
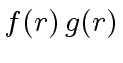 .
Observe that the cost of defining
.
Observe that the cost of defining ![]() by the values
by the values
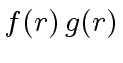 is
is 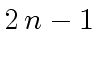 , which is cheap!
, which is cheap!
However if we need information about ![]() such as its
leading coefficient or its number of terms we need to
compute the coefficients of
such as its
leading coefficient or its number of terms we need to
compute the coefficients of ![]() .
The cost of this construction is in
.
The cost of this construction is in
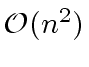 .
.
The underlying idea of the fast polynomial multiplication based
on the discrete Fourier transform is the following.
Assume that there exists a subset ![]() of
of ![]() with
with
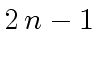 elements such that
elements such that
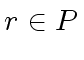 can be done
at nearly linear time cost (such as
can be done
at nearly linear time cost (such as
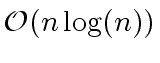 ),
),
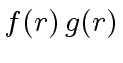 for
for 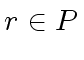 can be done
at nearly linear time cost.
can be done
at nearly linear time cost.
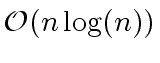 .
.
Such sets ![]() do not always exist. This depends on the ring
do not always exist. This depends on the ring ![]() and the degrees of the polynomials
and the degrees of the polynomials ![]() and
and ![]() .
However many finite fields possess such sets for small enough degrees
of
.
However many finite fields possess such sets for small enough degrees
of ![]() and
and ![]() .
For the arbitrary ring
.
For the arbitrary ring ![]() , it can be shown that the multiplication
of
, it can be shown that the multiplication
of ![]() nad
nad ![]() , represented by their
coefficients, can be done in
, represented by their
coefficients, can be done in
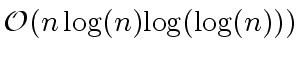 .
.