Definition 4
Let 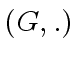 be a (multiplicative) group with neutral element
be a (multiplicative) group with neutral element 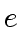 .
A nonempty subset
.
A nonempty subset
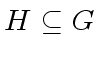 is a subgroup of
is a subgroup of 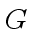 if the following three statements hold
if the following three statements hold
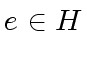 ,
,
- for every
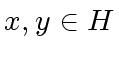 we have
we have
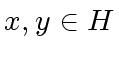 ,
,
- for every
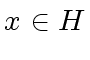 the inverse
the inverse 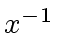 of
of 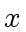 belongs to
belongs to 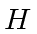 .
.
Theorem 3
For every subgroup 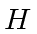 of the additive abelian group
of the additive abelian group
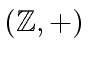 there exists an element
there exists an element
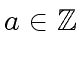 such that
such that 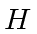 is the set
of the multiples of
is the set
of the multiples of 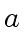 , that is
, that is
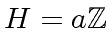 .
.
Theorem 4
Let 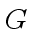 be a multiplicative group with neutral element
be a multiplicative group with neutral element 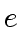 .
Let
.
Let 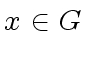 an element and gr(
an element and gr(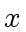 )
the subgroup of
)
the subgroup of 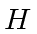 consisting of all powers of
consisting of all powers of 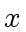 (including
(including
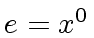 and
and 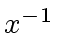 the inverse of
the inverse of 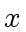 ).
Let
).
Let
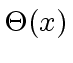 be the order of gr(
be the order of gr(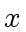 ),
that is the cardinality of gr(
),
that is the cardinality of gr(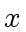 ).
Then two cases arise
).
Then two cases arise
- either gr(
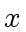 ) is infinite and then the powers
of
) is infinite and then the powers
of 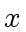 are pairwise different and thus
are pairwise different and thus 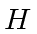 is isomorphic to
is isomorphic to
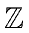 .
.
- or gr(
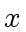 ) is finite and we have the following properties
) is finite and we have the following properties
-
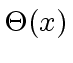 is the smallest integer
is the smallest integer 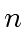 such that
such that 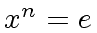 ,
,
-
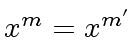 iff
iff
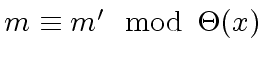 ,
,
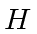 is isomorphic to
is isomorphic to
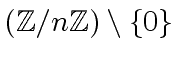 where
where
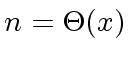 ,
,
-
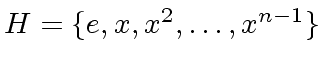 where
where
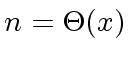 .
.
Marc Moreno Maza
2008-01-07
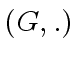 be a (multiplicative) group with neutral element
be a (multiplicative) group with neutral element 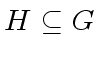 is a subgroup of
is a subgroup of 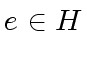 ,
,
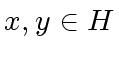 we have
we have
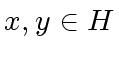 ,
,
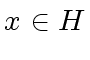 the inverse
the inverse 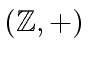 there exists an element
there exists an element
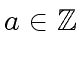 such that
such that 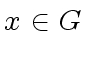 an element and gr(
an element and gr(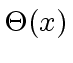 be the order of gr(
be the order of gr(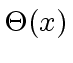 is the smallest integer
is the smallest integer 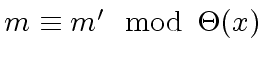 ,
,
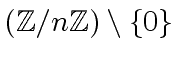 where
where
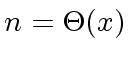 ,
,
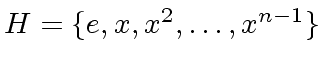 where
where
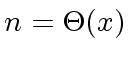 .
.