Next: Linear Hensel Lifting Up: Foundations of Computer Algebra: Hensel Previous: Foundations of Computer Algebra: Hensel
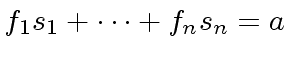 |
(1) |
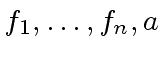 are given in
are given in 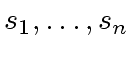 are unknowns in
are unknowns in
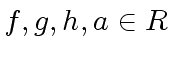 such that
such that
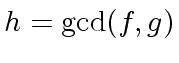 .
We consider the linear Diophantine equation
.
We consider the linear Diophantine equation
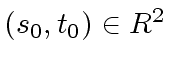 is a solution of Equation (2),
then
is a solution of Equation (2),
then 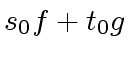 , divides also
, divides also 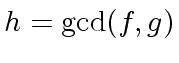 divides
divides 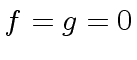 and also
and also 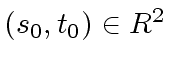 be computed by the Extended Euclidean Algorithm
applied to
be computed by the Extended Euclidean Algorithm
applied to 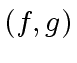 , such that we have
, such that we have
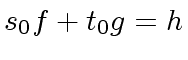 .
Then
.
Then
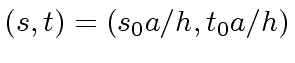 is a solution of
Equation (2).
is a solution of
Equation (2).
Now we prove 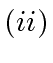 . Assume
. Assume 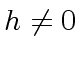 and let
and let
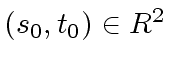 is a solution of
Equation (2).
Since
is a solution of
Equation (2).
Since 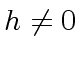 , then
, then 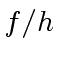 and
and 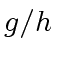 are coprime.
Let
are coprime.
Let 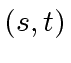 be in
be in ![]() .
Then we have
.
Then we have
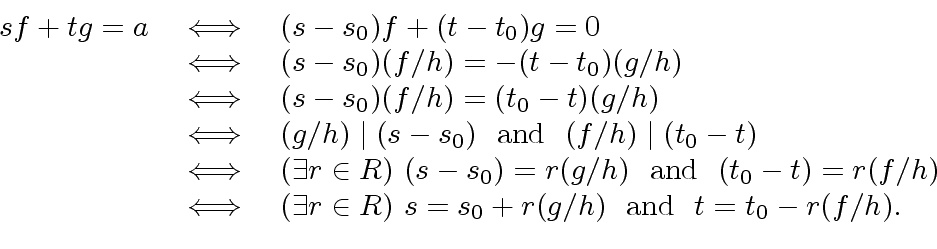 |
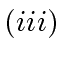 . Let
. Let
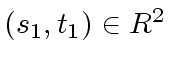 be a solution of
Equation (2).
Let
be a solution of
Equation (2).
Let 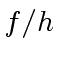 .
Hence we have
.
Hence we have
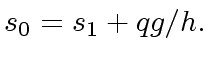 |
(7) |
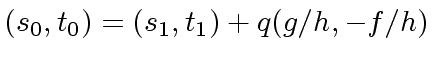 |
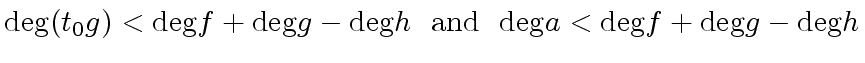 |
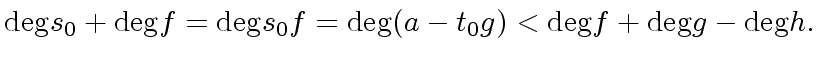 |
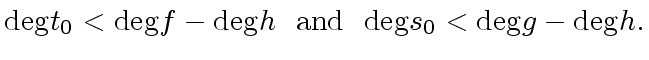 |
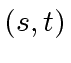 be a solution of Equation (2).
We know that there exists
be a solution of Equation (2).
We know that there exists 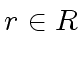 such that
such that
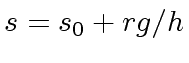 .
Since
.
Since
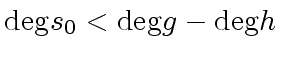 holds, if
holds, if 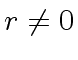 , we have
, we have
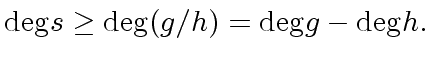 |
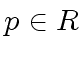 .
...
.
...Marc Moreno Maza