Next: Rational numbers. Up: How to encode the elements Previous: How to encode the elements
One machine word can contain a SINGLE PRECISION
INTEGER in the range
![$ [0, 2^{N} - 1]$](img168.png) .
To represent integers outside of this range, so called
MULTIPRECISION INTEGER, we use arrays of
.
To represent integers outside of this range, so called
MULTIPRECISION INTEGER, we use arrays of ![]() -bit words.
To be precise we consider the
-bit words.
To be precise we consider the ![]() -ary (or radix
-ary (or radix ![]() )
expansion of a nonzero integer:
)
expansion of a nonzero integer:
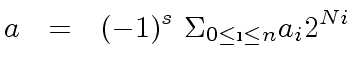 |
(33) |
![$ a_i \in [0, 2^{N} - 1]$](img171.png) is a digit in
the
is a digit in
the 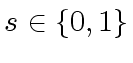 determines the sign of
determines the sign of ![$ n + 1 \in [1, 2^{N}]$](img173.png) is the number of
is the number of 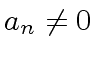 .
.

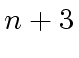 since we need
since we need
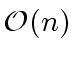 word operations
word operations
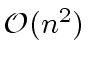 word operations.
word operations.
Marc Moreno Maza