Next: Real algebraic numbers. Up: How to encode the elements Previous: Rational numbers.
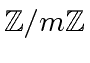 and even more for the fields
and even more for the fields
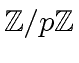 (where
(where 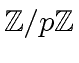 .
Here are some examples.
.
Here are some examples.
![$ [2, 2^{N} - 1]$](img186.png) we can use single integers.
Multiplication and addition can be made
in
we can use single integers.
Multiplication and addition can be made
in
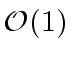 word operations.
N.B. multiplication requires a two single integers buffer
unless
word operations.
N.B. multiplication requires a two single integers buffer
unless ![$ [2, 2^{N-1} - 1]$](img188.png) .
Exponentiation and computation of inverses require a bit
more of works but are still in
.
Exponentiation and computation of inverses require a bit
more of works but are still in
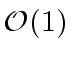 word operations.
For instance here's an ALDOR code
for the division of two integers modulo a third one
word operations.
For instance here's an ALDOR code
for the division of two integers modulo a third one
mod_/(i: %, j: %, n: %): % == {
local c0, d0, c1, d1: %;
(c0, d0) := (j, n);
(c1, d1) := (1, 0);
while not zero? d0 repeat {
q := c0 quo d0;
(c0, d0) := (d0, c0 - q*d0);
(c1, d1) := (d1, c1 - q*d1)
}
if c0 ~= 1 then error "inverse does not exist";
if c1 < 0 then c1 := c1 + n;
mod_*(i, c1, n);
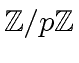 is a cyclic group. In other words, there exists
a generator
is a cyclic group. In other words, there exists
a generator
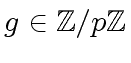 such that
every nonzero
such that
every nonzero
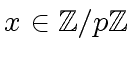 is a power of
is a power of 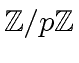 .
Then exponentiation and computation of inverses
become much more easy (for inverses we use Little Fermat
Theorem) than with the previous encoding.
However addition requires the use of tables
of logarithms and exponentiations, for efficiency.
Again all arithmetic operations are in
.
Then exponentiation and computation of inverses
become much more easy (for inverses we use Little Fermat
Theorem) than with the previous encoding.
However addition requires the use of tables
of logarithms and exponentiations, for efficiency.
Again all arithmetic operations are in
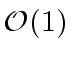 word operations.
word operations.
Marc Moreno Maza