Next: Asymptotically fast algorithms Up: What are our requirements for Previous: Post-facto extensions
(^)(x: %, n: NonNegativeInteger): % ==
(n < 0) =>
error "power: negative exponent";
n = 0 => 1;
n = 1 => x;
n = 2 => x*x;
-- General code.
i: SingleInteger := 0;
l: SingleInteger := length n;
u: % := 1;
repeat {
if bit(n, i) then u := u * x;
if i >= l then break;
x := x * x;
i := i + 1;
}
u
}
Assume that in the interface MONOID the exponentiation
has been defined as above.
In the MONOID
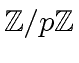 (where
(where 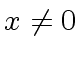 we have
we have
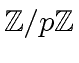 by something like
by something like
(^)(x: %, n: NonNegativeInteger): % == {
n := positiveRemainder(n,p);
zero? n => 1;
one? x => x;
local acc: %;
if odd? n then acc := x else acc := 1;
repeat {
n := shift(n,-1);
zero? n => return acc;
x := (x * x) mod p;
if odd? n then acc := (acc * x) mod p;
}
}
This will be made possible by INHERITANCE.
In a polynomial ring ![$ R[x]$](img156.png) one can do better too in some
special cases depending on the coefficient ring, as we have seen before.
This will be made possible by CONDITIONAL IMPLEMENTATION.
one can do better too in some
special cases depending on the coefficient ring, as we have seen before.
This will be made possible by CONDITIONAL IMPLEMENTATION.
Marc Moreno Maza