Next: Experimentation Up: Asymptotically fast algorithms Previous: Asymptotically fast algorithms
Let 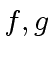 be two univariate polynomials in
be two univariate polynomials in ![]() with degrees
with degrees
![]() and
and ![]() respectively.
Let
respectively.
Let
![]() be their ring of coefficients.
Define
be their ring of coefficients.
Define
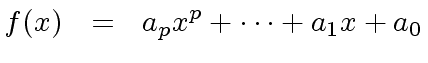 |
(39) |
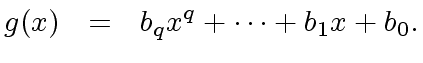 |
(40) |
COMPUTING THE PRODUCT 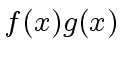 by the straightforward method requires
by the straightforward method requires
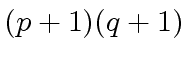 multiplications in
multiplications in
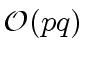 (in term of operations in
(in term of operations in
Thus the complexity of the computation of the product
of two univariate polynomials of degree at most ![]() is
is
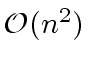 (in term of operations in
(in term of operations in
![]() ).
).
COMPUTING THE SUM
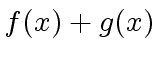 is
is
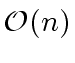 (in term of operations in
(in term of operations in
![]() )
if
)
if ![]() and
and ![]() have of degree at most
have of degree at most ![]() .
.
ADDING IS OFTEN CHEAPER THAN MULTIPLYING.
So adding polynomials is cheaper than multiplying them.
For many rings
![]() addition is also cheaper than multiplication.
So when computing
addition is also cheaper than multiplication.
So when computing 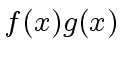 let's try to save on the number of
multiplications in
let's try to save on the number of
multiplications in
![]() .
.
THE KARATSUBA'S TRICK.
Assume ![]() and
and ![]() have degree
(strictly) less than
have degree
(strictly) less than ![]() (where
(where ![]() is an integer).
The Karatsuba's trick computes the product
is an integer).
The Karatsuba's trick computes the product 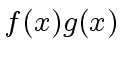 as follows.
as follows.
 of
of
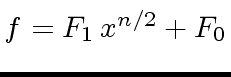 and
and
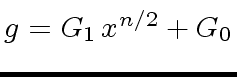 where
where
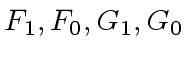 have degree
have degree 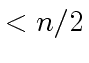 .
.
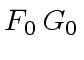 ,
,
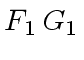 ,
,
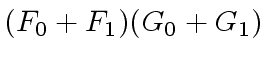 recursively
recursively
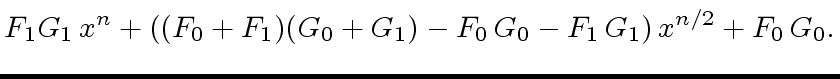 |
(41) |
ITS COMPLEXITY.
Let us count how many operations in
![]() we perform with the Karatsuba's trick.
we perform with the Karatsuba's trick.
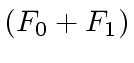 and
and
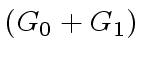 .
.
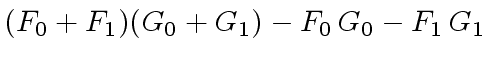
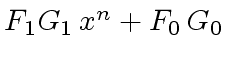 .
.
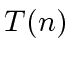 ) with
) with
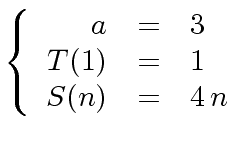 |
(42) |
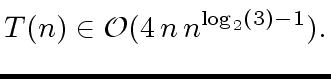 |
(43) |
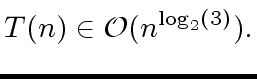 |
(44) |
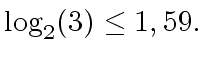 |
(45) |