Next: Bibliography Up: Symbolic Newton Iteration Previous: Linear Newton Iteration
Let ![]() be a commutative ring with units.
Let
be a commutative ring with units.
Let 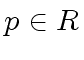 and
and
![$ {\phi} \in R[y]$](img64.png) .
We are concerned with solving the equation
.
We are concerned with solving the equation
![$ {\phi} \in R[y]$](img64.png) and let
and let 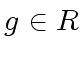 be such that
be such that
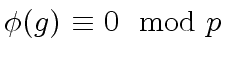 |
(30) |
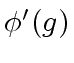 is invertible modulo
is invertible modulo 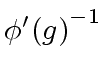 its inverse.
Consider an element
its inverse.
Consider an element 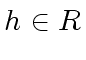 such that
such that
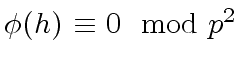 ,
,
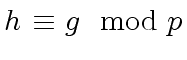 ,
,
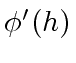 is invertible modulo
is invertible modulo
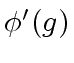 is invertible modulo
is invertible modulo 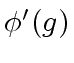 is invertible modulo
is invertible modulo ![[*]](crossref.png) computes
computes
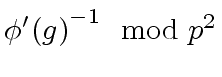 given
given
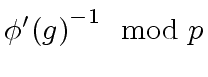 .
.
Since ![]() divides
divides ![]() , the following congruence holds
, the following congruence holds
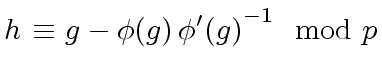 |
(32) |
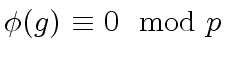 , this leads to
, this leads to
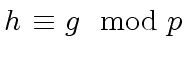 |
(33) |
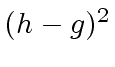 we obtain
we obtain
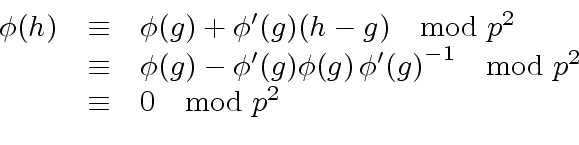 |
(34) |
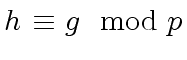 implies
implies
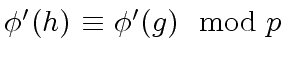 .
Indeed
.
Indeed ![$ R[x]$](img202.png) .
Therefore,
.
Therefore,
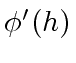 is invertible modulo
is invertible modulo 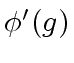 is invertible modulo
is invertible modulo
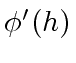 is invertible modulo
is invertible modulo 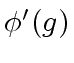 modulo
modulo 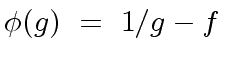 |
(35) |
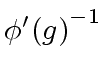 modulo
modulo
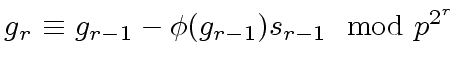 .
Then we have
.
Then we have
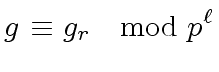 |
(36) |
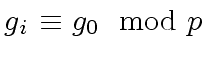 ,
,
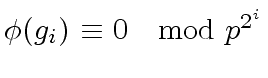 ,
,
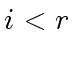 then
then
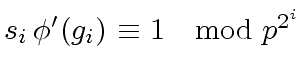 .
.
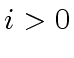 holds.
Then by induction hypothesis
holds.
Then by induction hypothesis
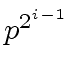 divides
divides
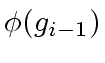 and
and
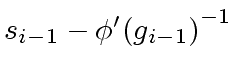 .
Then
.
Then 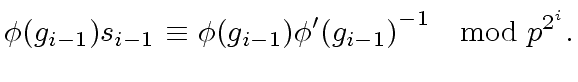 |
(37) |
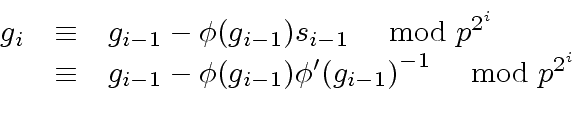 |
(38) |
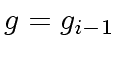 ,
, 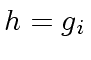 and
and
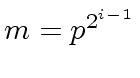 we obtain the first two invariants.
In addition, this leads to
we obtain the first two invariants.
In addition, this leads to
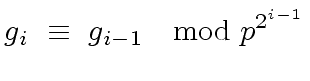 |
(39) |
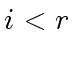 .
This implies
.
This implies
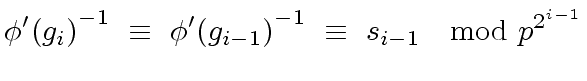 |
(40) |
![[*]](crossref.png) ).
Therefore the third invariant follows.
).
Therefore the third invariant follows.
Marc Moreno Maza