Next: Relation between gcds in and Up: Advanced Computer Algebra: The resultant Previous: Advanced Computer Algebra: The resultant
![$ {\mbox{${\mathbb{Q}}$}}[x]$](img8.png)
We saw in the first chapter that running the Euclidean
Algorithm in
![$ {\mbox{${\mathbb{Q}}$}}[x]$](img8.png) can lead to a significant expression swell.
Let us try to estimate how coefficients grow.
That is, we want to estimate the maximal space
needed to store one coefficient of an intermediate polynomial.
Let
can lead to a significant expression swell.
Let us try to estimate how coefficients grow.
That is, we want to estimate the maximal space
needed to store one coefficient of an intermediate polynomial.
Let ![]() be the number of bits of a machine word.
be the number of bits of a machine word.
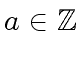 we define
we define
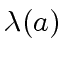 the length of
the length of
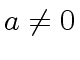 we have
we have
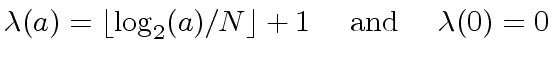 |
(1) |
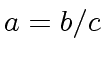 with
with
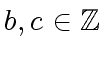 and
and
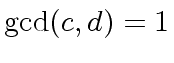 we define
we define
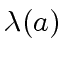 , the length of
, the length of 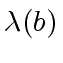 and
and
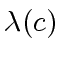 .
.
![$ a \in {\mbox{${\mathbb{Q}}$}}[x]$](img20.png) of degree
of degree 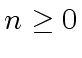 such that all coefficients have denominator
such that all coefficients have denominator 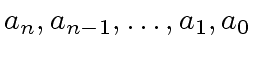 have gcd 1
then we define the length of
have gcd 1
then we define the length of 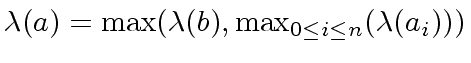 |
(2) |
![$ a \in {\mbox{${\mathbb{Q}}$}}[x]$](img20.png) of degree
of degree  can be represented with
can be represented with
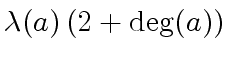 |
(3) |
 be univariate polynomials over
be univariate polynomials over
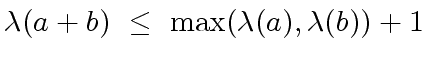 .
.
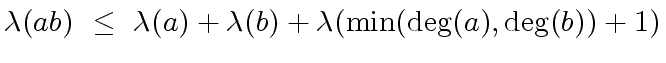 .
.
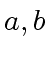 be univariate polynomials over
be univariate polynomials over
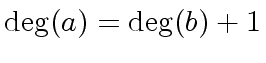 holds.
Let
holds.
Let 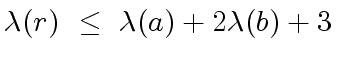 |
(4) |
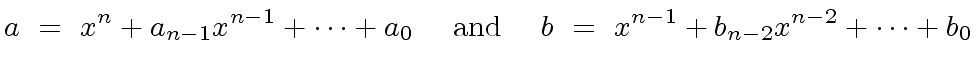 |
(5) |
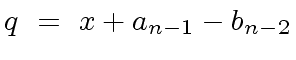 |
(6) |
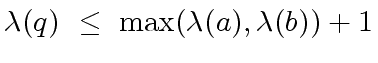 |
(7) |
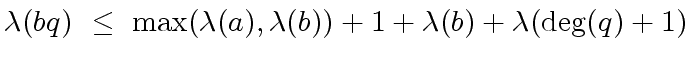 |
(8) |
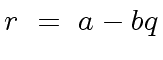 |
(9) |
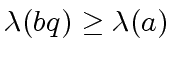 we obtain
we obtain
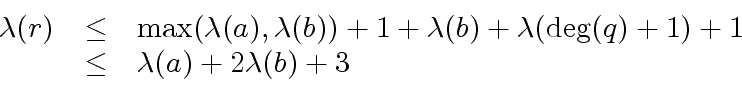 |
(10) |
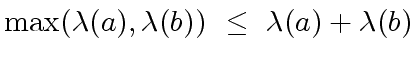 and
and
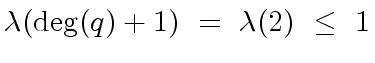 .
.
![$ a, b \in {\mbox{${\mathbb{Q}}$}}[x]$](img45.png) such that
such that
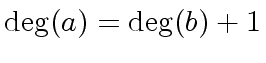 .
See [GG99].
These results provide us with an exponential upper bound for the
coefficient of the gcd computed by the Euclidean Algorithm.
But in fact a polynomial bound can be established.
Moreover there is an efficient modular approach for computing gcds in
.
See [GG99].
These results provide us with an exponential upper bound for the
coefficient of the gcd computed by the Euclidean Algorithm.
But in fact a polynomial bound can be established.
Moreover there is an efficient modular approach for computing gcds in
![$ {\mbox{${\mathbb{Q}}$}}[x]$](img8.png) and
and
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) as we shall see in the next sections.
as we shall see in the next sections.
Marc Moreno Maza