Next: A modular Gcd Algorithm in Up: Advanced Computer Algebra: The resultant Previous: Mignotte's factor bound
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png)
![$ f,g \in {\mbox{${\mathbb{Z}}$}}[x]$](img322.png) .
Before proving this algorithm, let us check
that all its computations are well defined.
Consider an iteration of the loop.
We assume that we have a source of primes large enough.
Given a prime
.
Before proving this algorithm, let us check
that all its computations are well defined.
Consider an iteration of the loop.
We assume that we have a source of primes large enough.
Given a prime 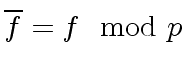 and
and
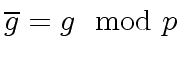 which implies that
the each coefficient
which implies that
the each coefficient ![$ [ - \frac{p-1}{2}, \frac{p-1}{2}]$](img326.png)
![$ {{\mbox{${\mathbb{Z}}$}}/{\langle p \rangle}}[x]$](img327.png) (same remark for the coefficients of
(same remark for the coefficients of ![$ w \in Z[x]$](img328.png) such that
such that
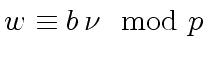 (same remark for the coefficients of
(same remark for the coefficients of 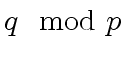 where
where 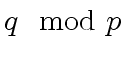 where
where 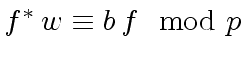 and
and
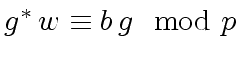 .
They hold since
.
They hold since 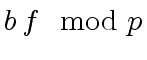 and
and
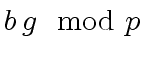 .
.
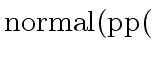 w
w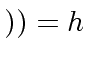 .
If the conditions hold then
.
If the conditions hold then
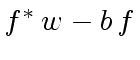 satisfies
satisfies
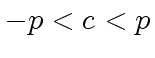 .
Whereas Relation (102) tells us that
every coefficient
.
Whereas Relation (102) tells us that
every coefficient 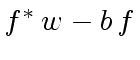 is a multiple of
is a multiple of 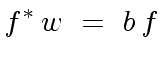 |
(103) |
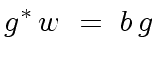 |
(104) |
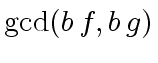 .
Hence the primitive part of
.
Hence the primitive part of 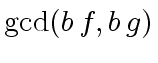 which is
which is 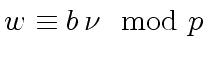 holds and since
holds and since 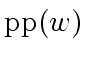 and
and 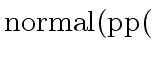 w
w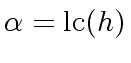 .
Since
.
Since 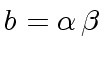 .
Hence we have
.
Hence we have
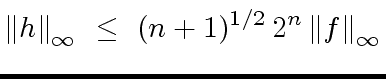 |
(108) |
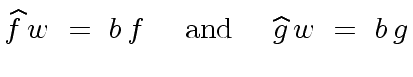 |
(111) |
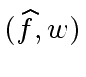 (as factors of
(as factors of 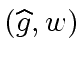 (as factors of
(as factors of 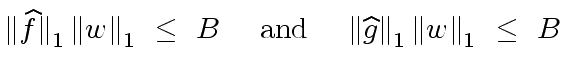 |
(112) |
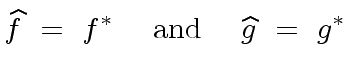 |
(113) |
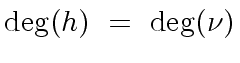 we derive Relation (105).
Together with the fact that
we derive Relation (105).
Together with the fact that 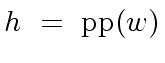 .
.
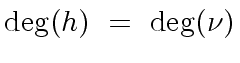 does not hold
Moreover for those prime such
does not hold
Moreover for those prime such
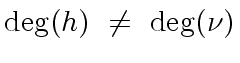 the polynomial
the polynomial
Marc Moreno Maza