You must implement a generator of random univariate polynomials
parametrized by the desired degree and the coefficient ring.
In MAPLE
- there is already a generator of random univariate polynomials,
- and you may choose to write one generator per desired coefficient ring.
In AXIOM
- there is less support for generating random polynomials,
- but it is still quite easy.
For each coefficient ring, the degree 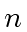 should vary from
should vary from 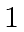 to a value large enough (typically
to a value large enough (typically 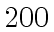 ) in order to show
that the Karatsuba's algorithm is asymptotically faster.
For each value of
) in order to show
that the Karatsuba's algorithm is asymptotically faster.
For each value of 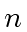 , it is recommended
, it is recommended
- to pick several random pairs and run both algorithms for this pair,
- to compute the average time for each algorithm.
Both MAPLE and AXIOM have graphical facilities
that you can use for displaying your experimental results.
You may also use gnuplot or any other tool that you
are familiar with.
Marc Moreno Maza
2008-01-07