Next: About this document ... Up: Quiz2 Previous: Exercise 2.
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img50.png) .
We assume that
.
We assume that 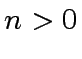 and that
and that 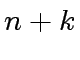 whith
whith 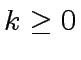 .
We define
.
We define
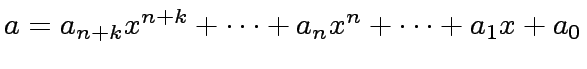 and
and
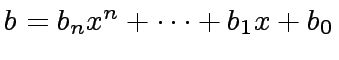 .
We are interesting in computing the remainder
.
We are interesting in computing the remainder ![$ {\mbox{${\mathbb{Q}}$}}[x]$](img57.png) ), by a modular method.
Let
), by a modular method.
Let 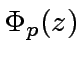 in
in
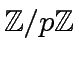 .
We extend this application to a map denoted
.
We extend this application to a map denoted ![$ {\mbox{${\mathbb{Z}}$}}[x]$](img50.png) to
to
![$ {\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}[x]$](img63.png) , such that
, such that ![$ {\mbox{${\mathbb{Z}}$}}[x]$](img50.png) , that is
no fractions appears during the computations.
, that is
no fractions appears during the computations.
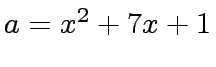 and
and 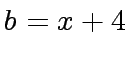 . Compute
. Compute 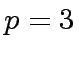 . Compute
. Compute
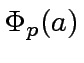 and
and
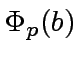 .
Then compute the quotient and the remainder of
.
Then compute the quotient and the remainder of
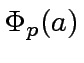 by
by
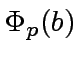 .
.
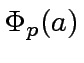 by
by
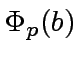 ?
?
Marc Moreno Maza