Next: Formula: the Chinese Remaindering Theorem Up: Quiz8 Previous: Guidelines.
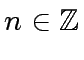 the set of the multiples of
the set of the multiples of 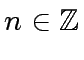 the residue class of the binary relation
the residue class of the binary relation
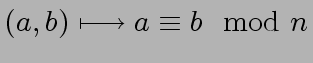 is denoted by
is denoted by
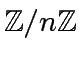 , as usual.
For a ring
, as usual.
For a ring
![$ {\mbox{${\mathbb{A}}$}}[x]$](img12.png) the ring of univariate polynomials
in
the ring of univariate polynomials
in Marc Moreno Maza