The goal of this exercise is to understand how
the fast division with remainder is slow
when the underlying polynomial multiplication is
not fast.
Let 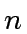 be a non-negative integer. Let
be a non-negative integer. Let
![$ g \in R[x]$](img26.png) be a polynomial of degree less than
be a polynomial of degree less than 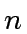 and let
and let
![$ f \in R[x]$](img15.png) be a polynomial of degree less than
be a polynomial of degree less than 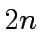 .
For this exercise, we rely on classical ``quadratic''
polynomial multiplication. Hence, we ignore all the tricks
(Karatsuba, FFT) learnt in class.
.
For this exercise, we rely on classical ``quadratic''
polynomial multiplication. Hence, we ignore all the tricks
(Karatsuba, FFT) learnt in class.
- Using classical arithmetic what is the number of operations
in
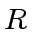 for computing
for computing
 .
.
- Using classical arithmetic what is the number of operations
in
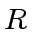 for computing
for computing
 .
.
- Deduce a (sharp) upper bound for the algorithm recalled on the
first page.
- Deduce a (sharp) upper bound for the (not so) fast division
with remainder when applied to a pair of polynomials
in
![$ R[x]$](img30.png) with respective degrees
with respective degrees 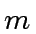 and
and 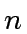 , assuming that
, assuming that
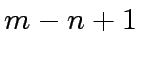 is a power of
is a power of 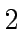 .
.
- Compare with classical division.
Answer 3

Answer 4

Answer 5

Answer 6

Marc Moreno Maza
2008-01-31
![]() be a non-negative integer. Let
be a non-negative integer. Let
![$ g \in R[x]$](img26.png) be a polynomial of degree less than
be a polynomial of degree less than ![]() and let
and let
![$ f \in R[x]$](img15.png) be a polynomial of degree less than
be a polynomial of degree less than ![]() .
For this exercise, we rely on classical ``quadratic''
polynomial multiplication. Hence, we ignore all the tricks
(Karatsuba, FFT) learnt in class.
.
For this exercise, we rely on classical ``quadratic''
polynomial multiplication. Hence, we ignore all the tricks
(Karatsuba, FFT) learnt in class.
 .
.
 .
.
![$ R[x]$](img30.png) with respective degrees
with respective degrees 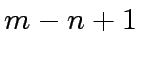 is a power of
is a power of