Exercise 4

The goal of this exercise is to write a desk calculator for regular languages. The user can

• either define a regular language by means of a regular expression,
• or submit a query about a defined language.

The representation of a defined language in the desk calculator is a finite automaton. Nota bene. We assume in the rest of the text that these automata are deterministic and complete (leading to the use of an error state). However you can use non-deterministic automata with or without instantaneous transitions. In that case you should adapt the specifications of the desk calculator.

The syntax of the definition of a language is

variable := language

where

• variable stands for an identifier (use the pattern of the second exercise)
• language is of one of the six forms
  • language $\bf\mid$ language
  • language $\bf .$ language
  • language $\bf {}^{\ast}$
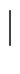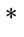
  • ( language )
  • variable
  • { expression }
  where expression is a regular expression (in the sense of the course) over the alphabet 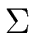$\Sigma$ consisting of the lower cases letters and the digits.

The possible queries are

The in

query which asks whether a word belongs or not to a language. The syntax is

"word" in language

where word is a word (in the mathematical sense) over 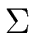$\Sigma$ and in is a keyword.

The states

query which asks what are the states of the automaton representing the language. The syntax is

states language

The initial

state query which asks what is the initial state of the automaton representing the language. The syntax is

initial language

The finals

query which asks what are the final states of the automaton representing the language. The syntax is

finals language

Here's a session with such a desk calculator. The prompt for the input line is ? and the prompt for the output line is =.

? L1 := {a(a|b)*}
= defined L1
? L2 := {(a|b)*b}
= defined L2
? L3 := L1.L2
= defined L3
?  "abba" in L3
= false
?  "abbab" in L3
= true
? states L3
= [0,1,2,error]
? initial L3
= 0
? finals L3
= [2]
? transitions L3
= (0, a, 1), (0, b, error), (1, a, 1),
  (1, b, 2), (2, a, 1), (2, b, 2)

We give now a more detailed description of the possible commands by illustrative examples.

L1 := {a}

Assigns L1 to the language consisting of the single word a.

L2 := L1*

Assigns L2 to the star of the language L1. Hence L2 consists of all possible sequences of a, including the empty word.

L3 := L1.L2

Assigns L3 to the product of the languages L1 and L2. Hence L3 consists of all possible sequences of a, except the empty word.

L4 := {b}

Assigns L4 to the language consisting of the single word b.

L5 := L1|L4

Assigns L5 to the union of the languages L1 and L4. Hence L5 consists of the words a and b.

"" in L3

Returns true iff the empty word belongs to L3. In our context the answer will be false.

"aaa" in L3

Returns true iff the word aaa belongs to L3 which is the case in our context.

states L5

Returns a list of the states of the automaton representing L5. This could be [0, 1 , error].

initial L5

Returns the initial state of the automaton representing L5. This could be 0.

finals L5

Returns the final states of the automaton representing L5. This could be [1].

transitions L5

Returns the transitions of the automaton representing L5. This could be (0, a, 1), (0, b, 1), (1, a, error), (1, b, error).