

Next: Data-flow analysis: reaching definitions
Up: Compiler Theory: Code Optimization
Previous: Data-flow Analysis and Global Optimization
A LOOP L IN A CONTROL FLOW GRAPH G is a subgraph satisfying the following properties.
- There exists a path from any node of L to any other node of L.
- There is only one node h of L such that there exists a node
n of G which is not a node of L and (n, h) is an edge of G.
This node h is called the entry point
or the header of the loop.
A loop that contains no other loop is called an inner loop.
To identify loops we need the following two notions.
IN A CONTROL FLOW GRAPH G, A DOMINATOR for a node n is a node d such that any path from
the entry of the CFG to n goes through d.
In this case we also say that d dominates n.
Algorithm 2
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $G$\ a CF...
...cap}_{ \ p \in N \ \mid \ (p,n) \in E} \ D(p)$\ \\
\end{tabbing}\end{minipage}}](img3.png)
- This algorithm terminates since
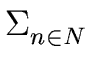 | D(n) |
cannot decrease infinitely many times.
| D(n) |
cannot decrease infinitely many times.
- The correctness of the algorithm can be made easily by induction
on the maximal length of an elementary path from n to n0.
Observe that the header h of a loop L dominates all other
nodes of L. Otherwise it cannot be the only entry point.
A BACK EDGE IN A CFG G is an edge (p, d ) of G such that d dominates p.
To each back edge one can associate a loop as follows.
THE NATURAL LOOP OF A BACK EDGE (n, d ) is a loop of its CFG computed
by the following algorithm.
Algorithm 3
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $G$\ a CF...
...\sf push}($p,stack$) \\
\> {\bf return} $N_L$\ \\
\end{tabbing}\end{minipage}}](img5.png)
Example 3
Consider the following TAC fragment.
|
s:=0 |
|
i:=0 |
|
n:=10 |
|
L1: |
t1 := a-b |
|
ifz t1 goto L2 |
|
t2 := i*4 |
|
s := s+t2 |
|
goto L3 |
|
L2: |
s := s+i |
|
L3: |
i := i+1 |
|
t3 := n-i |
|
ifnz t3 goto L1 |
|
t4 := a-b |
Its control flow graph is shown on Figure 2.
There is one back edge: (B5, B2).
Its natural loop consists of the nodes
B2, B3, B4, B5.
Figure 2:
A control flow graph with two loops.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.45]{ControlFlowGraph2.eps}
\end{figure}](img6.png) |
Occasionally it is difficult to determine when a loop is nested.
LOOP OPTIMIZATIONS often involve
- moving code out of the loop or
- pre-computing values for use in the loop
To do so, we need a basic block in which we insert such code
- before any loop optimization we create a new block
which is inserted immediately before the header
- such a block is called a pre-header
REDUCIBLE CONTROL FLOW GRAPHS. A control flow graph G is said to be reducible
if the removal of its back edges leads to an acyclic graph
where each node can be reached from the initial node of G.
In this case, all the edges of this acyclic graph are called forward edges.
Figure 3:
A control flow graph which is not reducible.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.45]{ControlFlowGraph3.eps}
\end{figure}](img7.png) |
Figure 3 shows a control flow graph which
is not reducible.
Indeed it has no loops (in the sense of the above definition)
and it is not acyclic.
Figure 4 sketches a simple
algorithm for determining whether a control flow graph
is non-reducible. When no more reductions are possible,
the initial CFG is reducible if and only if the reduced
CFG consists only of a single node.
Figure 4:
Determining whether a control flow graph is reducible or not.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.45]{ControlFlowGraph5.eps}
\end{figure}](img8.png) |
In the first situation, one can contract the nodes 1 and 2
since it is allowed to arrive at 2 only from 1.
In the second case, one is allowed to remove the loop (in the sense
of graph theory) around the node.
One can show the following properties about reducible CFG
- Non-reducible flow graphs arise basically only from unstructured use of goto-statements
(jumps into the middle of a loop from the outside of the loop,
without using the header).
- The key property of reducible control flow graphs
is that any set of nodes that intuitively appears as a loop,
contains a back edge.
- Thus we only need to identify the back edges
to find all loops in a reducible control flow graph.
Figure 5 sketches a technique of node-splitting
for dealing with the improper regions of non-reducible graphs.
Figure 5:
Dealing with improper regions by node-splitting.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.45]{ControlFlowGraph6.eps}
\end{figure}](img9.png) |


Next: Data-flow analysis: reaching definitions
Up: Compiler Theory: Code Optimization
Previous: Data-flow Analysis and Global Optimization
Marc Moreno Maza
2004-12-02
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $G$\ a CF...
...cap}_{ \ p \in N \ \mid \ (p,n) \in E} \ D(p)$\ \\
\end{tabbing}\end{minipage}}](img3.png)
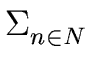 | D(n) |
cannot decrease infinitely many times.
| D(n) |
cannot decrease infinitely many times.