

Next: Data-flow analysis: available expressions.
Up: Compiler Theory: Code Optimization
Previous: Data-flow analysis: reaching definitions
Many optimizations and user code introduce copy statements of the form
s: x := y
It is sometimes possible to eliminate such copy statements.
COPY PROPAGATION CONDITIONS. Assume that for a statement u where x is used
- statement s is the only definition of x reaching u
- on every path from s to u there are no assignments to y
Then we may substitute y for x in u.
Observe that
- we know how to check the first condition,
- but not the second one ...
We shall set up
- a new data-flow analysis together with
- new data-flow equations to solve this problem.
COPY REACHING A POINT. Let s: x := y be a copy statement and p be a point of the TAC program 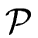 .
We say that the copy s: x := y reaches p if
every path
.
We say that the copy s: x := y reaches p if
every path 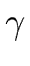 from the initial node of
from the initial node of 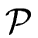 to p
to p
- contains s: x := y
- and subsequent to the last occurrence of s: x := y on
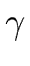 there is no assignment to y or x.
there is no assignment to y or x.
This implies that the statement s: x := y reaches the point p.
COPY PROPAGATION DATA-FLOW SETS. For a basic block B
- inC(B) is the set of the copies (from anywhere in
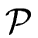 ) reaching entry(B).
) reaching entry(B).
- outC(B) is the set of the copies (from anywhere in
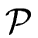 ) reaching exit(B).
) reaching exit(B).
- genC(B) is the set of the copies defined in B and reaching exit(B).
- A copy statement s: x := y is killed in B if
- s: x := y
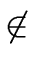 B and
B and
- x or y are assigned in B.
- killC(B) is the set of the copy statements (from anywhere in
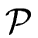 ) that are killed in within block B by a redefinition of y or x.
) that are killed in within block B by a redefinition of y or x.
Observe that
- inC(B) can contain only one copy statement with
a given x on the left.
Observe that for every basic block B
- the data-flow sets genC(B) and killC(B) can be computed easily,
- the definitions of genC(B) and killC(B) essentially deals
with graph theory and will not detect copy statements that are never hit (= evaluated),
- so we may apply the following precautionary principles
- we add a copy statement to genC(B) only if we are sure that it is hit,
- we add a copy statement to killC(B) even if it is doubtful that it will be killed.
DATA-FLOW EQUATIONS For every basic block B the data-flow sets inC(B) and outC(B) satisfy
the following equations
| inC(B) |
= |
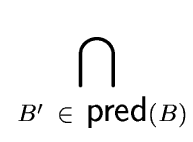 outC(B'), outC(B'), |
| outC(B) |
= |
genC(B) 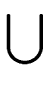  inC(B) inC(B) 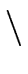 killC(B) killC(B)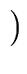 . . |
|
(6) |
COMPUTING THE DATA-FLOW SETS FOR THE COPY PROPAGATION PROBLEM Assume that the set C of all copy statements in 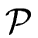 has been computed.
Then, for each basis block B one can compute genC(B) and killC(B).
Now set
has been computed.
Then, for each basis block B one can compute genC(B) and killC(B).
Now set
inC(B1) = 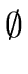 and outC(B1) = genC(B1) and outC(B1) = genC(B1) |
(7) |
where B1 is the first block
Then one can set up a completion algorithm
initializing every for basic block
B 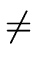 B1
B1
and using the updating equations
| outC(B) |
= |
genC(B)  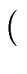 inC(B) inC(B) 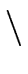 killC(B) killC(B)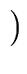 . . |
| inC(B) |
= |
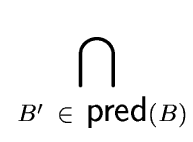 outC(B'), outC(B'), |
|
(9) |


Next: Data-flow analysis: available expressions.
Up: Compiler Theory: Code Optimization
Previous: Data-flow analysis: reaching definitions
Marc Moreno Maza
2004-12-02
![]() .
We say that the copy s: x := y reaches p if
every path
.
We say that the copy s: x := y reaches p if
every path ![]() from the initial node of
from the initial node of ![]() to p
to p
![]() has been computed.
Then, for each basis block B one can compute genC(B) and killC(B).
Now set
has been computed.
Then, for each basis block B one can compute genC(B) and killC(B).
Now set