

Next: Finite Automata.
Up: Finite Automata
Previous: Non-deterministic Finite Automata
NFA WITH INSTANTANEOUS TRANSITIONS. A non-deterministic finite automaton with
instantaneous transitions
(or
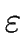 -transitions) consists of six things:
-transitions) consists of six things:
- an input alphabet
 ,
,
- a finite set S whose elements are called states,
- a set
I
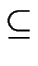 S of distinguished states, called initial states,
S of distinguished states, called initial states,
- a set
F
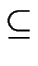 S of distinguished states, called accepting states,
S of distinguished states, called accepting states,
- a function
 from
S×
from
S× to 2S, thus every state-symbol couple
is mapped by
to 2S, thus every state-symbol couple
is mapped by  to a subset of S,
to a subset of S,
- a function
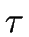 mapping each state of S
to a subset of S
mapping each state of S
to a subset of S
such that
( , S, I, T,
, S, I, T, ) is a NFA.
The functions
) is a NFA.
The functions  and
and 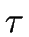 are called
the non-instaneous transition function
and
the
are called
the non-instaneous transition function
and
the
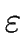 -transition function
(or the instaneous transition function).
Such an automaton will be called a NFAIT or an
-transition function
(or the instaneous transition function).
Such an automaton will be called a NFAIT or an
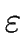 -NFA, for short.
-NFA, for short.
Figure 7:
A non-deterministic finite automaton with instantaneous transitions.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{DFAandNFAIT-1.eps}
\end{figure}](img31.png) |
INSTANTANEOUS TRANSITIONS.
Observe that
- The goal of the function
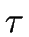 is to describe transitions
from one state to others without reading any letter.
One can view also these
is to describe transitions
from one state to others without reading any letter.
One can view also these
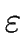 -transitions from one state
to others as transitions obtained after reading the empty word
-transitions from one state
to others as transitions obtained after reading the empty word
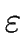 .
.
- In the transition graph of a NFAIT
the
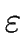 -transitions are indicated by edges
(from one state to another) labeled by
-transitions are indicated by edges
(from one state to another) labeled by
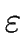 .
.
Figure 8:
A NFAIT
accepting
L1  L2
L2  L3
L3  L4.
L4.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.4]{1epsilonAutomatonFor4.eps}
\end{figure}](img32.png) |
THE LANGUAGE ACCEPTED BY A NFAIT. For
A 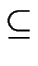 S we define the
S we define the
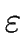 -closure of
A as the set of the states that can be reached from a
state of A by reading the empty word
-closure of
A as the set of the states that can be reached from a
state of A by reading the empty word
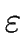 .
The
.
The
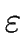 -closure of A is denoted by
-closure of A is denoted by
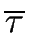 (A)
and is formally defined by Algorithm 2.
(A)
and is formally defined by Algorithm 2.
Algorithm 2
- 1
- toSee := A;
- 2
-
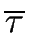 (A) := A;
(A) := A;
- 3
- while
toSee
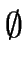 repeat
repeat
- 3.1
- s := first(toSee); toSee := rest(toSee);
- 3.2
- for
s'

 (s) repeat
(s) repeat
- 3.2.1
- if
(s'
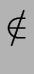 toSee) and
(s'
toSee) and
(s' 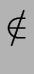
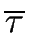 (A)) then toSee := cons(s', toSee);
(A)) then toSee := cons(s', toSee);
- 3.3
-
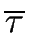 (A) := cons(
s,
(A) := cons(
s,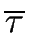 (A));
(A));
- 4
- return(
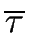 (A))
(A))
For two states s and s', and for a word w
we define the relation
s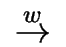 s'
by induction on the length | w| of w:
s'
by induction on the length | w| of w:
- if
w =
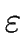 we have
s
we have
s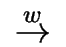 s'
for every
s'
s'
for every
s' 
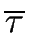 ({s}),
({s}),
- if w = vx where v is a word and x is a letter, we have
s
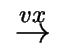 s'''
if there exist s', s'' such that
s
s'''
if there exist s', s'' such that
s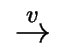 s',
s''
s',
s'' 
 (s', x) and
s'''
(s', x) and
s''' 
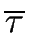 ({s''}).
({s''}).
a word w over  is accepted (or recognized)
by the NFAIT
is accepted (or recognized)
by the NFAIT  if there exists an initial
state i and a final state f such that
i
if there exists an initial
state i and a final state f such that
i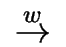 f.
f.
FROM A NFAIT TO A DFA ACCEPTING THE SAME LANGUAGE.
Theorem 2
Let

= (

,
S,
I,
T,

,
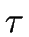
)
be a NFAIT and let
L be the language
accepted by

.
Then there exists a DFA
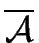
which accepts
L too.
To construct such an
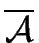 one proceeds as in
Algorithm 1 with the following
two modifications.
one proceeds as in
Algorithm 1 with the following
two modifications.
- The initial state is
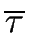 (I)
instead of
(I)
instead of
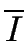 .
.
- The transition
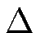 (A, x) is defined by:
(A, x) is defined by:
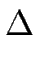
(
A,
x) =
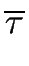
({
s' | (
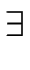 s
s 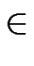 A
A) (
s' 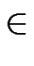
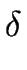
(
s,
x))}).
The resulting algorithm is called again the subset algorithm.
Figure 9 shows a DFA accepting the same language
as the NFAIT of Figure 7. This DFA is computed
by means of the subset algorithm.
Let us describe the construction of the transition table of this DFA.
- 1.
- The initial state is the
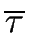 (I) =
(I) = 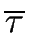 (1) = 134.
The transitions from it are
(1) = 134.
The transitions from it are
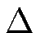 (134, a) = 2,
(134, a) = 2,
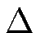 (134, b) =
(134, b) = 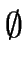
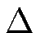 (134, c) =
(134, c) = 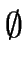 .
This shows that
.
This shows that 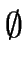 and 2 are states of the output DFA.
The
and 2 are states of the output DFA.
The 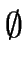 has to be understood as the error-state.
If we do not need to produce a complete DFA
then we can discard this error-state.
has to be understood as the error-state.
If we do not need to produce a complete DFA
then we can discard this error-state.
- 2.
- The transition from state 2 are
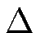 (2, a) = 2,
(2, a) = 2,
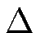 (2, b) = 1234
(2, b) = 1234
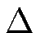 (2, c) = 1234.
This shows that 1234 is a state of the output DFA.
(2, c) = 1234.
This shows that 1234 is a state of the output DFA.
- 3.
- The transition from state 1234 are
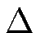 (1234, a) = 2,
(1234, a) = 2,
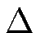 (1234, b) = 1234
(1234, b) = 1234
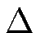 (1234, c) = 1234.
(1234, c) = 1234.
- 4.
- The final states of this DFA are its states
which contain at least one of the final states
of the input NFA. Hence the final states are
134 and 1234.
Therefore we obtain the following transition table.
| |
a |
b |
c |
| 134 |
2 |
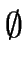 |
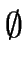 |
| 2 |
2 |
1234 |
1234 |
| 1234 |
2 |
1234 |
1234 |
Figure 9:
From a NFAIT to a DFA accepting the same language and
produced by the subset algorithm.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.4]{DFAandNFAIT-3.eps}
\end{figure}](img43.png) |
REMARKS ABOUT THE NFAIT-TO-DFA CONSTRUCTION.
- If the input NFAIT (of the subset algorithm) has q
states then the output DFA has
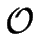 (2q) states.
(2q) states.
- However the states of the DFA computed by this
algorithm have the following property:
they can all be reached on some input word.
In other words, none of these computed states is useless.
- In practice, the number of reachable states
(of the output DFA) is much smaller
than the above exponential upper bound.
- However the DFA constructed by the above algorithm
is not necessarily minimal: it is possible
that the number of states can be further reduced.
Figure 10 shows a DFA
recognizing the same language as the DFA
of Figure 4 but using
6 states instead of 9.
Figure 10:
A minimal DFA
accepting
L1  L2
L2  L3
L3  L4.
L4.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{1minimalDFAFor4.eps}
\end{figure}](img45.png) |


Next: Finite Automata.
Up: Finite Automata
Previous: Non-deterministic Finite Automata
Marc Moreno Maza
2004-12-02
![]() -transitions) consists of six things:
-transitions) consists of six things:
![]() S we define the
S we define the
![]() -closure of
A as the set of the states that can be reached from a
state of A by reading the empty word
-closure of
A as the set of the states that can be reached from a
state of A by reading the empty word
![]() .
The
.
The
![]() -closure of A is denoted by
-closure of A is denoted by
![]() (A)
and is formally defined by Algorithm 2.
(A)
and is formally defined by Algorithm 2.
![]() s'
by induction on the length | w| of w:
s'
by induction on the length | w| of w:
![]() one proceeds as in
Algorithm 1 with the following
two modifications.
one proceeds as in
Algorithm 1 with the following
two modifications.