

Next: Languages recognized by finite automata
Up: Finite Automata
Previous: Non-deterministic Finite Automata with instantaneous
Because any non-deterministic finite automaton (with or without
instantaneous transitions) can be replaced by a deterministic
finite automaton recognizing the same language, from now on
we will just say finite automaton (FA for short) instead of
DFA, NFA or NFAIT. In practice, we will use
- NFAs or NFAITs for designing an automaton on the paper and then
- DFAs for implementing it on computer.
Indeed, NFAs and NFAITs are easier to manipulate
but DFAs are closer to computer programs.
Finally we will make the following simplification
in the notations for NFAIT:
we will denote the non-instaneous transition function
and
the
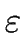 -transition function
with the same letter.
More precisely, let
(
-transition function
with the same letter.
More precisely, let
(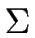 , S, I, T,
, S, I, T,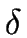 ,
,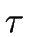 ) be a NFAIT.
We define for every s
) be a NFAIT.
We define for every s 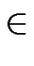 S
S
With this convention we can give an unified definition
for DFA, NFA or NFAIT.
A FINITE AUTOMATON over 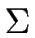 is a 5-uple
(
is a 5-uple
(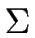 , S, I, T,
, S, I, T,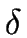 ) where
) where
- S is a finite set, called the set of states of the FA,
- I anf T are non-empty subsets of S,
called the sets of the initial states and accepting states
of the FA, respectively,
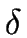 is a map from
S×(
is a map from
S×(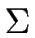
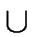 {
{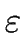 })
to 2S, called the transition function of the FA.
})
to 2S, called the transition function of the FA.
A non-empty word
w = x1x2 ... xn with length n is recognized by
the FA
(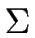 , S, I, T,
, S, I, T,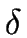 ) if there exist states
s1, s2, ... , sn-1
) if there exist states
s1, s2, ... , sn-1 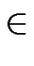 S such that
S such that
- the state s1 is an initial state,
- the state si+1 belongs to
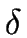 (si, xi)
for
i = 1 ... n-1,
(si, xi)
for
i = 1 ... n-1,
- the state sn-1 is an accepting state.
The empty word
w = 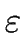 is recognized by the above FA if
is recognized by the above FA if
- either
I
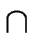 F
F 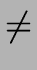
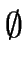
- or there exists an initial state s such that
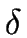 (s,
(s,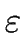 )
is an accepting state.
)
is an accepting state.


Next: Languages recognized by finite automata
Up: Finite Automata
Previous: Non-deterministic Finite Automata with instantaneous
Marc Moreno Maza
2004-12-02
![]() is a 5-uple
(
is a 5-uple
(![]() , S, I, T,
, S, I, T,![]() ) where
) where