

Next: Regular expressions
Up: Finite Automata
Previous: Finite Automata.
LANGUAGES RECOGNIZED BY FA. Let  be an alphabet.
A language L over
be an alphabet.
A language L over  is recognized by FA
if there exists a finite automaton
is recognized by FA
if there exists a finite automaton  such that L is the language recognized by
such that L is the language recognized by  .
.
THE PUNPING LEMMA. A natural question is
- are all languages over
 recognized by FA?
recognized by FA?
- and if no can we characterize those languages which
are recognized by FA?
To answer the first part of this question
we start with the following remark.
Proposition 1
Every language over

with a finite number
of words is recognized by FA.
Indeed let
L = {w1, w2,..., wn} be such
a language. We can easily make FAs
 1,
1,
 1, ...
1, ...
 n recognizing the languages
L1 = {w1},
L2 = {w1}, ...,
Ln = {wn},
respectively.
Then by using
n recognizing the languages
L1 = {w1},
L2 = {w1}, ...,
Ln = {wn},
respectively.
Then by using
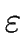 -transitions
we can construct a single FA
-transitions
we can construct a single FA  recognizing
recognizing
Therefore, if a language L is not recognized by FA
then it must contain an infinite number of words.
This leads us to the following remark.
Proposition 2
Let
L be a language recognized by FA
and with an infinite number of words.
Let

= (

,
S,
I,
T,

)
be a DFA accepting
L.
Then

possesses a
circuit.
In other words, there exist a positive integer
n
together with
n states
s1,
s2,...,
sn
and
n - 1 letters
x1,
x2,...,
xn-1
(not necessarily pairwise different) such that
- (i)
-
si+1 =
 (si, xi) for every
i = 1 ... n - 1,
(si, xi) for every
i = 1 ... n - 1,
- (ii)
-
si
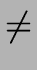 sj for
i, j = 1 ... n - 1 and i
sj for
i, j = 1 ... n - 1 and i 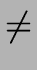 j,
j,
- (iii)
- s1 = sn.
Indeed, let s1 be the initial state,
q be the number of states of  and p the number of letters.
Since L is infinite,
there exists a word
w = x1 ... x
and p the number of letters.
Since L is infinite,
there exists a word
w = x1 ... x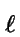 in L with lenght
in L with lenght
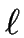 > q.
Recognizing w requires at least q + 1 transitions:
> q.
Recognizing w requires at least q + 1 transitions:
s2 = 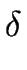 (s1, x1), s3 = (s1, x1), s3 = 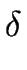 (s3, x3),...s (s3, x3),...s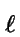 = = 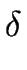 (s (s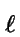 -1, x -1, x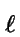 -1), s -1), s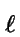 +1 = +1 = 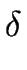 (s (s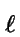 , x , x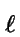 ). ). |
(4) |
At least two of the visited states si must be equal
and the proposition is proved.
Proposition 3 gives
a more precise statement of the above statement
and Figure 11 sketches its proof.
Proposition 3 (Pumping Lemma)
Let
L be a language recognized by FA
and with an infinite number of words.
Then there exists a positive integer
N
such that for every word
m  L
L with length
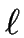
>
N
there exist three words
u,
v,
w such that
- (i)
-
m = u v w,
- (ii)
-
v
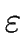 ,
,
- (iii)
- for every positive integer k we have
u vk w
 L.
L.
Figure 11:
Sketch of the pumping Lemma.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{pumpingLemma.eps}
\end{figure}](img51.png) |
Example 1
Let us apply Proposition
3
to the language
L = {
anbn} over

= {
a,
b}.
Let us assume that
L is recognized by FA.
Let
N,
m,
u,
v,
w be as in the proposition.
If
v counts more
a than
b then for
k big enough
u vk w will also have more
a than
b
and thus cannot belong to
L.
Similarly if
v counts more
b than
a then
u vk w cannot belong to
L for
k big enough.
So
v must be of the form
anbn.
But then for
k > 1 the word
u vk w does not
belong to
L.
Finally we are led to a contradiction and the language
L
is recognized by FA.
CONSTRUCTION OF LANGUAGES RECOGNIZED BY FA We would like now to characterize those languages which
are recognized by FA.
To address this question we give a series
of four propositions and one theorem.
Each of these four propositions provide a mechanism (or rule)
to build languages recognized by FA.
Theorem 3 states that these rules allow us to build
all possible languages recognized by FAs.
- Proposition 4 expresses the fact
that languages consisting of a single word consisting itself
of a single letter are recognized by FA.
This statement is an obvious consequence
of the previous Proposition 1
and is illustrated by
Figure 12.
- Proposition 5 expresses the fact
that the union of two languages recognized by FA
is itself recognized by FA.
This statement is also trivial and was illustrated by
Figure 4.
- Proposition 6 expresses the fact
that the concatenation (or product) of two languages recognized by FA
is also recognized by FA.
This statement is also not difficult to prove
and we have already used this result implicitely
with most examples.
- Proposition 7
expresses the fact that the star of a language recognized by
FA is also recognized by FA.
The star (or Kleene closure) of a language
is defined and illustrated below.
Proposition 4
For every
x 


the language
L = {
x}
consisting of the single word
w =
x is recognized by FA.
Figure 12:
A DFA
accepting a language consisting of a single letter.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{singleLetterLanguage.eps}
\end{figure}](img52.png) |
To illustrate Proposition 5,
6 and
7
we will use the concept of a normalized FA.
NORMALIZED FINITE AUTOMATA A finite automaton
 = (
= ( , S, I, F,
, S, I, F, )
is normalized if it satisfies to the following properties
)
is normalized if it satisfies to the following properties
 has only one initial state, say s,
has only one initial state, say s,
 has only one final (= accepting) state, say f,
has only one final (= accepting) state, say f,
- no transition leads to the initial state s, or more formally, for every
t
 S and every
x
S and every
x 

 {
{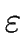 }
we have
s
}
we have
s 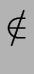
 (t, x),
(t, x),
- no transition leaves from the final state f, or more formally, for every
x


 {
{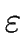 }
we have
}
we have
 (f, x) =
(f, x) = 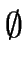 .
.
Normalized FA are generally depicted
as shown on Figure 13.
Figure 13:
A normalized FA.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{normalizedFADiagram.eps}
\end{figure}](img53.png) |
Figure 14:
Normalized FAs for R0 languages.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{normalizedFAofR0Language.eps}
\end{figure}](img54.png) |
THE UNION OF TWO LANGUAGES RECOGNIZED BY FA is a language recognized by FA.
Proposition 5
formulates this statement with DFAs
and Figure 15
illustrates it with normalized FAs.
Figure 15:
A normalized FA accepting the sum of two other normalized FAs.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.4]{sumOfNormalizedFA.eps}
\end{figure}](img55.png) |
Proposition 5
Let
L1 and
L2 be two languages over

recognized by the DFAs
 1
1 = (

,
S1,
s1,
F1,
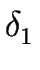
)
and
 2
2 = (

,
S2,
s2,
F2,
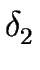
) respectively.
Let us assume that
S1 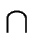 S2
S2 =
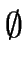
.
(If this is not the case then we can
rename the states of
 2
2.)
Then, the language
L1  L2 is recognized by the NFA
L2 is recognized by the NFA
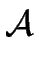 1+2 = ( 1+2 = (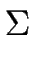 , S1 , S1 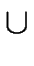 S2,{s1, s2}, F1 S2,{s1, s2}, F1 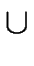 F2, F2,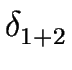 ) ) |
(5) |
where the transition function
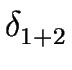
is defined as follows
for every
x 

and for every
s  S1
S1  S2
S2
THE PRODUCT OF TWO LANGUAGES RECOGNIZED BY FA is a language recognized by FA.
Proposition 6
formulates this statement with DFAs
and Figure 16
illustrates it with normalized FAs.
Figure 16:
A normalized FA accepting the sum of two other normalized FAs.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.4]{productOfNormalizedFA.eps}
\end{figure}](img64.png) |
Proposition 6
Let
L1 and
L2 be two languages over

recognized by the DFAs
 1
1 = (

,
S1,
s1,
F1,
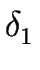
)
and
 2
2 = (

,
S2,
s2,
F2,
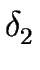
) respectively.
Again, let us assume that
S1 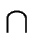 S2
S2 =
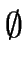
.
We denote by L1L2 (or L1.L2) the language consisting of
all words of the form w1w2 (concatenation of w1 and w2)
where w1 and w2 belong to L1 and L2 respectively.
This language is called the PRODUCT LANGUAGE of L1 by L2
Then, the language L1L2 is recognized by the NFA
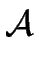 1.2 = ( 1.2 = (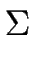 , S1 , S1 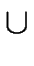 S2,{s1}, F2, S2,{s1}, F2,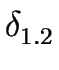 ) ) |
(7) |
where the transition function
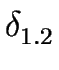
is defined as follows
for every
x 


{
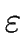
} and for every
s  S1
S1  S2
S2
KLEENE CLOSURE OF A LANGUAGE. Let  be an alphabet and let w be a word over
be an alphabet and let w be a word over  .
Let n be a non-negative integer.
First we define the n-th power of w, denoted by wn, as follows:
.
Let n be a non-negative integer.
First we define the n-th power of w, denoted by wn, as follows:
wn = 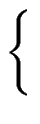 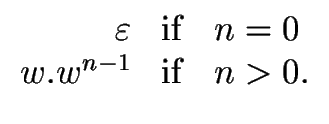 |
(9) |
Let L be a language over  .
Now we define the n-th power of L, denoted by Ln, as follows:
.
Now we define the n-th power of L, denoted by Ln, as follows:
Ln =  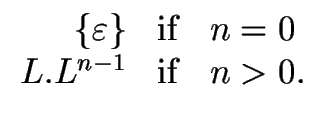 |
(10) |
Then we define the star (or Kleene closure)
of L, denoted by L * , as the union
of all powers of L, that is
L * = 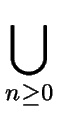 Ln. Ln. |
(11) |
Therefore, a word w over  belongs to L *
if
belongs to L *
if
- either w is the empty word
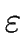
- or there exists a positive integer n and a word
u such that w = un.
Figure 17:
A DFA accepting a language L and
a NFAIT accepting the star of L.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.4]{starOfAnAutomaton.eps}
\end{figure}](img74.png) |
We give now some useful formulas.
Let L and M be two languages over  .
Observe that
.
Observe that
-
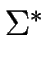 is the set of all words over
is the set of all words over  .
.
- Let L+ be the union of all Ln with n > 0.
Then
L+ = L.L * .
- If
L
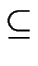 M then
L *
M then
L * 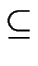 M * .
M * .
- For every non-negative integer n we ahve
L * n = L * .
-
L * * = L * .
-
(L * + M * ) * = (L * .M * ) * .
-
(L * + M * ) * = (L + M) * .
THE KLEENE CLOSURE OF A LANGUAGE RECOGNIZED BY FA is a language recognized by FA.
Proposition 7
formulates this statement with DFAs
and Figure 18
illustrates it with normalized FAs.
Figure 18:
A normalized FA accepting the star of another normalized FA.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.4]{starOfNormalizedFA.eps}
\end{figure}](img76.png) |
Proposition 7
Let
L be a language over

recognized by the
DFA

= (

,
S,
s0,
F,

).
Then L * is recognized by the NFA
where the transition function
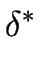
is defined as follows
for every
x 


{
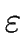
} and for every
s  S
S
KLEENE THEOREM. We denote by
R0( ) the set of all
languages of the form {x} for
x
) the set of all
languages of the form {x} for
x 

 {
{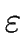 }.
Then for a positive integer n we define
Rn(
}.
Then for a positive integer n we define
Rn( )
as the set of languages over
)
as the set of languages over  consisting of
consisting of
- the languages of
Rn-1(
 ),
),
- the languages of the form L + M for
L, M
 Rn-1(
Rn-1( ),
),
- the languages of the form L.M for
L, M
 Rn-1(
Rn-1( ),
),
- the languages of the form L * for
L
 Rn-1(
Rn-1( ).
).
Obviously, for every non-negative integer n,
every language member of
Rn( ) is recognized by FA.
The theorem of Kleene studies the opposite direction.
) is recognized by FA.
The theorem of Kleene studies the opposite direction.
Theorem 3 (Kleene)
Let
L be a language recognized by FA.
Then there exists a non-negative integer
n
such that
L belongs to
Rn(

).
This suggests the introduction of the notion
of a regular expression.


Next: Regular expressions
Up: Finite Automata
Previous: Finite Automata.
Marc Moreno Maza
2004-12-02
![]() be an alphabet.
A language L over
be an alphabet.
A language L over ![]() is recognized by FA
if there exists a finite automaton
is recognized by FA
if there exists a finite automaton ![]() such that L is the language recognized by
such that L is the language recognized by ![]() .
.
![]() 1,
1,
![]() 1, ...
1, ...
![]() n recognizing the languages
L1 = {w1},
L2 = {w1}, ...,
Ln = {wn},
respectively.
Then by using
n recognizing the languages
L1 = {w1},
L2 = {w1}, ...,
Ln = {wn},
respectively.
Then by using
![]() -transitions
we can construct a single FA
-transitions
we can construct a single FA ![]() recognizing
recognizing
![]() and p the number of letters.
Since L is infinite,
there exists a word
w = x1 ... x
and p the number of letters.
Since L is infinite,
there exists a word
w = x1 ... x![]() in L with lenght
in L with lenght
![]() > q.
Recognizing w requires at least q + 1 transitions:
> q.
Recognizing w requires at least q + 1 transitions:
![]() = (
= (![]() , S, I, F,
, S, I, F,![]() )
is normalized if it satisfies to the following properties
)
is normalized if it satisfies to the following properties
![]() L2 is recognized by the NFA
L2 is recognized by the NFA
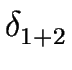 )
)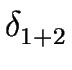 is defined as follows
for every
x
is defined as follows
for every
x 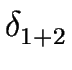 (s, x) =
(s, x) = 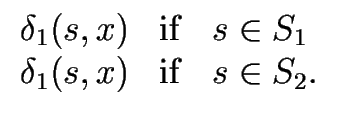
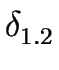 )
)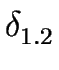 is defined as follows
for every
x
is defined as follows
for every
x 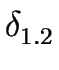 (s, x) =
(s, x) = 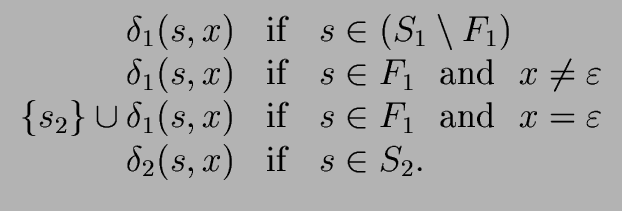
![]() be an alphabet and let w be a word over
be an alphabet and let w be a word over ![]() .
Let n be a non-negative integer.
First we define the n-th power of w, denoted by wn, as follows:
.
Let n be a non-negative integer.
First we define the n-th power of w, denoted by wn, as follows:
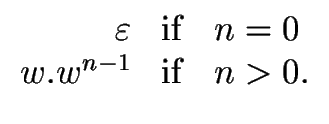
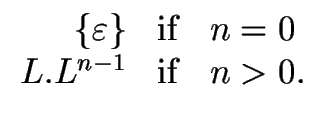
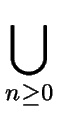 Ln.
Ln.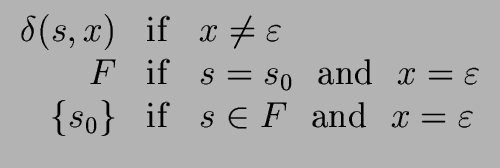
![]() ) the set of all
languages of the form {x} for
x
) the set of all
languages of the form {x} for
x ![]()
![]()
![]() {
{![]() }.
Then for a positive integer n we define
Rn(
}.
Then for a positive integer n we define
Rn(![]() )
as the set of languages over
)
as the set of languages over ![]() consisting of
consisting of