
Next: LR Parsers
Up: Parsing (II)
Previous: Parsing (II)
KEY IDEAS.
- The weakness of top-down LL(k) parsing techniques
is that they must predict which production to use,
having seen only the first k tokens in the right side.
- The more powerful techniques of bottom-up LR(k) parsing
is able to postpone the decision until it has seen
- input tokens corresponding to the entire
right side of the production
- and k lookahead tokens beyond
BOTTOM-UP PARSING constructs a parse tree for an input string beginning at the leaves
and working up towards the root.
- To do so, bottom-up parsing tries to find a rightmost derivation
of a given string backwards.
- Bottom-up parsing is also called shift-and-reduce parsing where
- shift means read the next token,
- reduce means that a substring
 matching the right side of a production
A
matching the right side of a production
A 
 is replaced by A.
is replaced by A.
HANDLE. Let
G = (VT, VN, S, P) be a context-free grammar.
Let n be a positive integer,
let
w, be two strings of symbols and let A be a nonterminal
such that
A
be two strings of symbols and let A be a nonterminal
such that
A 
 is a production of G.
We say that
(A
is a production of G.
We say that
(A 
 , n) is a handle for w if
there exists a string of symbols
, n) is a handle for w if
there exists a string of symbols 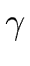 such that
such that
and such that
n = |  | + 1.
| + 1.
More informally, a handle of w is a substring  that matches a right
side of a production
A
that matches a right
side of a production
A 
 such that the reduction
of the handle corresponds to a step of the reverse of a rightmost derivation.
such that the reduction
of the handle corresponds to a step of the reverse of a rightmost derivation.
Theorem 4
Let
G = (
VT,
VN,
S,
P) be a context-free grammar.
If
G is unambiguous then for each string of symbols
w
such that
S 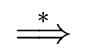 w
w there
exists exactly one handle.
Example 22
Consider the grammar
|
S |
 |
aSb |  |
- The handle of aabb is
(S

 , 3)
, 3)
- The handle of aaSbb is
(S
 aSb, 2)
aSb, 2)
- The handle of aSb is
(S
 aSb, 1)
aSb, 1)
Example 23
Consider the grammar
The string ac has handles
(A  a, 1) and
(B
a, 1) and
(B  a, 1).
So the grammar is ambiguous.
a, 1).
So the grammar is ambiguous.
Example 24
Consider the grammar
N.B. In the sentential form Ab the handle is
(B  b, 2)
and not
(S
b, 2)
and not
(S  A, 1).
A, 1).
HANDLE PRUNING is the general approach used
in shift-and-reduce parsing.
The implementation of handle pruning involves
the following data-structures:
- - a stack
- to hold the grammar symbols,
- - an input buffer
- containing the remaining input,
- - a table
- to decide handles.
Initially the situation is
where w is the sentence to parse.
The possible actions of a shift-and-reduce parser are:
- - shift
- where the next symbol is shifted onto the top of the stack
- - reduce
- where the parser
- knows that the right end of the handle is at the top of the stack,
- locates the left end of the handle within the stack and
- decide with what nonterminal to replace the handle.
- - accept
- where the parser announces successful completion of parsing.
- - error
- where the parser discovers that a syntax error has occured
and calls an error recovery routine.
The final configuration must be
Handle pruning can be implemented using a stack because
of the following fact.
Proposition 1
Let
G = (VT, VN, S, P) be an unambiguous context-free grammar.
In a shift-and-reduce parser for G implemented with a stack,
the right end of the handle will always appear on top
the stack.
Proof.
This fact becomes clear when considering the possible forms
of two successive steps in any rightmost derivation.
These two steps can be of the form (type 1)
or the form (type 2)
S 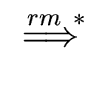 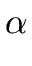 B x A z B x A z 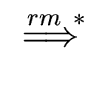 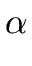 B x y z B x y z 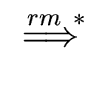 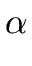 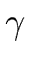 x y z x y z |
(48) |
- In type 1, first the rightmost nonterminal A
is replaced by the right side of the production
A

 B y
and then the rightmost nonterminal B is replaced by
the right side of the production
B
B y
and then the rightmost nonterminal B is replaced by
the right side of the production
B 
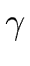 .
.
- In type 2, the rightmost nonterminal A is replaced first by use of the rule
A
 y (where y is a string of one or more terminals)
and then B is replaced by using
B
y (where y is a string of one or more terminals)
and then B is replaced by using
B 
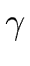 .
.
We proceed by induction.
Let us assume that the handle
B 
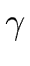
appears on top of the stack.
Then let us show that the handle
A 
 B y
B y in type 1
(and the handle
A  y
y in type 2) appears on top also.
Let us consider type 1 in reverse, where a shift-and-reduce parser has just reached
the following configuration.
The parser now reduces the handle.
| Stack |
Input |
  B B |
y z |
Since
B is the rightmost nonterminal, the right end of the
handle of
w =

 Byz
Byz
cannot be to the left of
B.
Therefore the parser can shift
y.
| Stack |
Input |
  B y B y |
z |
For case 2 in reverse, assume the following configuration has been reached
| Stack |
Input |
 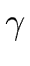 |
x y z |
Reduction leads to
| Stack |
Input |
 B B |
x y z |
Again
B is the rightmost nonterminal so it needs to be involved.



Next: LR Parsers
Up: Parsing (II)
Previous: Parsing (II)
Marc Moreno Maza
2004-12-02
 such that
such that
 is the leftmost factor of w such that
is the leftmost factor of w such that

 .
.
 by A in w.
by A in w.
 aABe
aABe  aAde
aAde  aAbcde
aAbcde  abbcde
abbcde