

Next: Implementing translation schemes with YACC
Up: Compiler Theory: Syntax-Directed Translation
Previous: Translation Schemes
As in the previous section, we enhance the notion of syntax-directed definitions
in order to specify the order of evaluation of the semantic rules.
This leads to the concept of a L-attributed definition.
KEY IDEAS. Both notions of translation scheme and L-attributed definition
are close. However
- the later provides more care for the treatment of inherited
attributed, leading to a more powerful theoretical concept.
- whereas the former is closer to a true computer program,
leading to a more practical concept.
THE DEPTH-FIRST EVALUATION ORDER. We consider a syntax-directed definition S and a parse tree T
for S showing the attributes of the grammar symbols of T.
Figure 1 shows an example of such a tree.
Algorithm 3
provides an order, called depth-first evaluation order,
for evaluating attributes shown by T.
Algorithm 3
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] A node $n...
...he synthesized attributes of $n$; \\
\> {\bf end}.
\end{tabbing}\end{minipage}}](img69.png)
Remark 3
We now introduce a class of syntax-directed definitions,
called L-attributed definitions, whose attributes
can always be evaluated in depth-first order.
- the L-attributed stands for one pass
from left-to-right.
- Intuitively, there are no right-to-left dependencies
between attribute occurrences in the productions.
- L-attributed definitions include all syntax-directed
definitions based on LL(1) grammars.
We will admit this statement.
L-ATTRIBUTED DEFINITIONS. A syntax-directed definition is L-attributed
if for each production
A  X1 ... Xn,
for each
j = 1 ... n,
each inherited attribute of Xj
depends only
X1 ... Xn,
for each
j = 1 ... n,
each inherited attribute of Xj
depends only
- the attributes of
X1 ... Xj-1,
- the inherited attributes of A.
Theorem 1
The attributes of an L-attributed definition
can always be evaluated in depth-first order.
Proof.
By induction on the depth of a parse tree
T.
Observe that a parse tree has at least depth 1 and two nodes.
If T has depth 1, then its root is labeled by S
and the associated production must have the form
S  a1 ... an where
a1,..., an
are terminals.
Recall that terminals do not have inherited attributes.
Observe that every synthesized attribute of a terminal
must be known in advance since semantic rules
are only associated with productions (and thus cannot
define a synthesized attribute of a terminal).
Moreover, observe also that any inherited attribute of S
must be known in advance, too.
Now Algorithm 3
computes the synthesized attributes of S
and thus evaluates all the attributes in T.
a1 ... an where
a1,..., an
are terminals.
Recall that terminals do not have inherited attributes.
Observe that every synthesized attribute of a terminal
must be known in advance since semantic rules
are only associated with productions (and thus cannot
define a synthesized attribute of a terminal).
Moreover, observe also that any inherited attribute of S
must be known in advance, too.
Now Algorithm 3
computes the synthesized attributes of S
and thus evaluates all the attributes in T.
Assume now that T has depth d > 1.
The production associated with the root has the form
S  X1 ... Xn where
X1,..., Xn
are grammar symbols.
Each subtree rooted at a child of S can be viewed
as a parse tree of a L-attributed definition.
However the root of each of these subtrees may have
inherited attributes that must be computed
(we cannot assume that they are some known constants).
X1 ... Xn where
X1,..., Xn
are grammar symbols.
Each subtree rooted at a child of S can be viewed
as a parse tree of a L-attributed definition.
However the root of each of these subtrees may have
inherited attributes that must be computed
(we cannot assume that they are some known constants).
Let j be in
1 ... n.
By virtue of the induction hypothesis and
by virtue of Algorithm 3
we can assume that all attributes of
X1,..., Xj-1 are known
Since the inherited attributes of S must be known constants,
by definition of an L-attributed syntax-directed definition
we can compute the inherited attributes of Xj.
When all inherited attributes of
X1,..., Xn
are computed, then it is clear that all synthesized attributes
of S can be computed.
Therefore Algorithm 3
evaluates all the attributes in T.

Example 9
The syntax-directed definition of the let language
is an L-attributed syntax-directed definition.
|
Production |
Semantic Rule |
S  E E |
E.env := initialEnv() |
E1   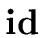 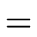 E2 E2 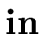 E3 E3 
|
E2.env := E1.env |
|
E3.env := Update(
E1.env,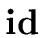 , E2.val) , E2.val) |
|
E1.val := E3.val |
E1  (E2 + E3) (E2 + E3) |
E1.val :=
E2.val + E3.val |
|
E2.env := E1.env |
|
E3.env := E1.env |
E  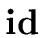 |
E.val := LookUp(
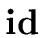 , E.env) , E.env) |
E  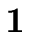 |
E.val := 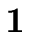 |
E  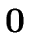 |
E.val := 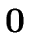 |
|
Production |
Semantic Rule |
A  L M L M |
L.i := f1(A.i) |
|
M.i := f2(L.s) |
|
A.s := f3(M.s) |
A  Q R Q R |
R.i := f4(A.i) |
|
Q.i := f5(R.s) |
|
A.i := f6(Q.s) |
 Q R.
Q R.
FROM L-ATTRIBUTED DEFINITIONS TO TRANSLATION SCHEMES. Every L-attributed definition can be converted
into a translation scheme that will always succeed
in evaluating the attributes in a parse tree,
provided that the following rules are observed.
Let
A  X1 ... Xn be any production
and j be in the range
1 ... n.
X1 ... Xn be any production
and j be in the range
1 ... n.
- Rule 1.
- The inherited attributes of Xj
must be computed in actions occurring
to the left of Xj in the translation.
(Indeed they may be needed when visiting
the subtree rooted at Xj.)
- Rule 2.
- An action can refer to a synthesized attribute Xj.s
of Xj only if Xj appears to the left of this action.
(Indeed Xj.s will be computed when visiting
the subtree rooted at Xj.)
- Rule 3.
- A synthesized attribute of A should be computed
in an action occurring at the end of the translation.
(Indeed all attributes of
X1,..., Xn may be needed.)
Example 10
The following translation scheme does not satisfy Rule 1.
|
S |
 |
A1 A2 {A1.in : = 1; A2.in : = 1} |
|
A |
 |
a {print(A.in)} |
S  {A1.in : = 1; A2.in : = 1} A1 A2 {A1.in : = 1; A2.in : = 1} A1 A2 |
A  a {print(A.in)} a {print(A.in)} |
Example 11
Consider the following syntax-directed definition for the
point size and height of boxes containing mathematical formulas.
|
Production |
Semantic Rule |
S  B B |
B.ps := 10 |
|
S.ht := B.ht |
B  B1 B2 B1 B2 |
B1.ps := B.ps |
|
B2.ps := B.ps |
|
B.ht := max(
B1.ht, B2.ht) |
B  B1 B1  B2 B2 |
B1.ps := B.ps |
|
B2.ps := shrink(B.ps) |
|
B.ht := disp(
B1.ht, B2.ht) |
B   |
B.ht :=
 .h×B.ps .h×B.ps |
- The nonterminal B represents a box which has been assigned to a mathematical formula.
- The production
B
 B B represents the juxtaposition of two boxes.
B B represents the juxtaposition of two boxes.
- When
B
 B1 B2 is applied,
B1 B2 is applied,
- the boxes B1 and B2 inherit
the point size of B,
- and the height of B represented by
the synthesized attribute B.ht is given by max(
B1.ht, B2.ht).
- The production
B
 B1
B1  B2 represents
a subscripted expression.
B2 represents
a subscripted expression.
- When
B
 B1
B1  B2 is applied,
B2 is applied,
- the shrink(B.ps) returns a fraction of the B.ps, say 30%,
- and disp(
B1.ht, B2.ht) allows for downward displacement
of the box B2 and computes the height of B.
Consider the production
S  B together with its semantic rules
B.ps := 10 and S.ht := B.ht.
B together with its semantic rules
B.ps := 10 and S.ht := B.ht.
- Rule 1 implies that the action {B.ps := 10} must occur
before B is visited.
- Rule 2 and Rule 3 imply that the action {S.ht := B.ht}
must occur after B is visited.
Consider the second production
B  B1 B2 together with its semantic rules
B1.ps := B.ps, B2.ps := B.ps and B.ht := max(
B1.ht, B2.ht).
B1 B2 together with its semantic rules
B1.ps := B.ps, B2.ps := B.ps and B.ht := max(
B1.ht, B2.ht).
- Rule 1 implies that the actions {B1.ps := B.ps}
and {B2.ps := B.ps} must occur before B1 and B2 are visited respectively.
- Rule 2 and Rule 3 imply that the action {B.ht := max
(B1.ht, B2.ht)}
must occur after B1 and B2 are visited.
Similar considerations with the other two productions lead to
the following translation scheme.
|
S |
 |
|
{B.ps := 10} |
|
|
B |
{S.ht := B.ht} |
|
B |
 |
|
{B1.ps := B.ps} |
|
|
B1 |
{B2.ps := B.ps} |
|
|
B2 |
{B.ht := max(
B1.ht, B2.ht) } |
|
B |
 |
|
{B1.ps := B.ps} |
|
|
B1 |
|
|
|
sub |
{ B2.ps := shrink(B.ps) } |
|
|
B2 |
{ B.ht := disp(
B1.ht, B2.ht) } |
|
B |
 |
text |
{ B.ht :=
 .h×B.ps } .h×B.ps } |
Example 12
To conclude this section we give a translation scheme
for the let language
|
S |
 |
|
{ E.env := initialEnv() } |
|
|
E |
|
|
E1 |
 |
|
{ E2.env := E1.env } |
|
|
   E2 E2
|
{ E3.env := Update(
E1.env,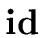 , E2.val) } , E2.val) } |
|
|
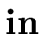 E3 E3 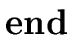
|
{ E1.val := E3.val } |
|
E1 |
 |
|
{ E2.env := E1.env } |
|
|
|
{ E3.env := E1.env } |
|
|
(E2 + E3)
|
{ E1.val :=
E2.val + E3.val } |
|
E |
 |
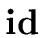 |
{ E.val := LookUp(
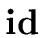 , E.env) } , E.env) } |
|
E |
 |
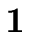 |
{ E.val := 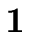 } } |
|
E |
 |
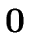 |
{ E.val := 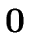 } } |


Next: Implementing translation schemes with YACC
Up: Compiler Theory: Syntax-Directed Translation
Previous: Translation Schemes
Marc Moreno Maza
2004-12-02
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] A node $n...
...he synthesized attributes of $n$; \\
\> {\bf end}.
\end{tabbing}\end{minipage}}](img69.png)
![]() X1 ... Xn,
for each
j = 1 ... n,
each inherited attribute of Xj
depends only
X1 ... Xn,
for each
j = 1 ... n,
each inherited attribute of Xj
depends only
![]() a1 ... an where
a1,..., an
are terminals.
Recall that terminals do not have inherited attributes.
Observe that every synthesized attribute of a terminal
must be known in advance since semantic rules
are only associated with productions (and thus cannot
define a synthesized attribute of a terminal).
Moreover, observe also that any inherited attribute of S
must be known in advance, too.
Now Algorithm 3
computes the synthesized attributes of S
and thus evaluates all the attributes in T.
a1 ... an where
a1,..., an
are terminals.
Recall that terminals do not have inherited attributes.
Observe that every synthesized attribute of a terminal
must be known in advance since semantic rules
are only associated with productions (and thus cannot
define a synthesized attribute of a terminal).
Moreover, observe also that any inherited attribute of S
must be known in advance, too.
Now Algorithm 3
computes the synthesized attributes of S
and thus evaluates all the attributes in T.
![]() X1 ... Xn where
X1,..., Xn
are grammar symbols.
Each subtree rooted at a child of S can be viewed
as a parse tree of a L-attributed definition.
However the root of each of these subtrees may have
inherited attributes that must be computed
(we cannot assume that they are some known constants).
X1 ... Xn where
X1,..., Xn
are grammar symbols.
Each subtree rooted at a child of S can be viewed
as a parse tree of a L-attributed definition.
However the root of each of these subtrees may have
inherited attributes that must be computed
(we cannot assume that they are some known constants).
![]()
![]() X1 ... Xn be any production
and j be in the range
1 ... n.
X1 ... Xn be any production
and j be in the range
1 ... n.