| (2) |
But what could we do if we had the three types
- There is no natural coercion between
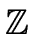 /p
/p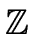 and
and
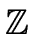 /m
/m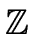 .
.
- So the type of an expression like 1 + 2 and consequently the signature of + may also depend on what is done with 1 + 2.
AN OVERLOADED OPERATOR may have different meanings depending upon its context.
| (2) |
SET OF POSSIBLE TYPES FOR A SUBEXPRESSION. The first step in resolving the overloading of operators and functions occuring in an expression E' is to determine the possible types for E'.
|
E' |
{ E'.types := | E.types } |
|
E |
{ E.types := | lookup(id.entry) } |
|
E |
{ E.types := |
{t | ( |
NARROWING THE SET OF POSSIBLE TYPES. The second step in resolving the overloading of operators and functions in the expression E' consists of
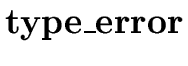 .
.
|
E' |
{ E.unique := | if E'.types = {t} | |
| then t | |||
else
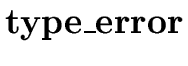 } } |
|||
| E | |||
| { E'.code := | E.code } | ||
|
E |
{ E.code := | generate(
|
|
|
E |
{ t := E.unique } | ||
| { S :=
{s |
|||
| { E2.unique := | if S = {s} | ||
| then s | |||
else
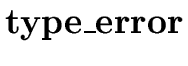 } } |
|||
| { E1.unique := | if S = {s} | ||
| then
s |
|||
else
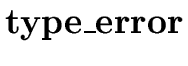 } } |
|||
| E1[E2] | |||
| { code := generate(apply':' E.unique) } | |||
| { E.code := | E1.code | | E2.code | | code |