

Next: Exercise 3.
Up: Quiz3
Previous: Exercise 1.
In the ring
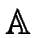 =
= 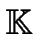 [x] of univariate polynomials
with coefficients in
[x] of univariate polynomials
with coefficients in
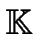 =
= 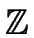 /17
/17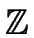 , we consider
the polynomials
f1 = x2 + 1,
g1 = x + 1,
f2 = x3 + x2 + x + 1 and
g2 = x2 + 3x + 1.
Using one of the FFT-based multiplication algorithms described
in the course notes:
, we consider
the polynomials
f1 = x2 + 1,
g1 = x + 1,
f2 = x3 + x2 + x + 1 and
g2 = x2 + 3x + 1.
Using one of the FFT-based multiplication algorithms described
in the course notes:
- compute the product of the polynomials f1 and g1
- compute the product of the polynomials f2 and g2
For each product, you should give (at least) the results of each
Discrete Fourier Transforms.
Of course, you should better choose primitive roots of unity that minize
the number of required operations in
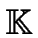 .
.
Answer 3

Answer 4

Answer 5

Answer 6



Next: Exercise 3.
Up: Quiz3
Previous: Exercise 1.
Marc Moreno Maza
2006-01-09
