- for all a, b
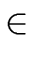 R with a
R with a 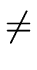 0 and b
0 and b 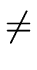 0 we have
d (a b)
0 we have
d (a b) 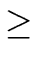 d (a),
d (a),
- for all a, b
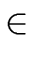 R with b
R with b 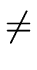 0
there exist q, r
0
there exist q, r 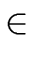 R such that
R such that
a = bq + r and d (r) < d (b). (1)
| a = bq + r and d (r) < d (b). | (1) |
| a = b q1 + r1 = b q2 + r2 with deg(r1) < deg(b) and deg(r2) < deg(b) | (2) |
| r1 - r2 = b (q1 - q2) with deg(r1 - r2) < deg(b) | (3) |
| R = {x + iy | x, y |
(4) |
|
(5) |
|
(6) |