

Next: How to encode the elements
Up: Implementing Computer Algebra: basic ideas
Previous: Implementing Computer Algebra: basic ideas
Obviously we need to implement the various usual sets of numbers:
- the ring of INTEGER NUMBERS
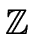 ,
,
- the field of RATIONAL NUMBERS
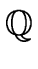 ,
,
- the rings of MODULAR INTEGERS
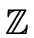 /n
/n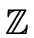 (and especially those which are prime fields),
(and especially those which are prime fields),
- the different sets of FLOATING POINT NUMBERS
(with fixed or arbitrary precision),
- the ordered ring of REAL ALGEBRAIC NUMBERS,
- and many others that we will discover later.
Clearly we need also:
- UNIVARIATE OR MULTIVARIATE
POLYNOMIALS over each of these sets of numbers,
- MATRICES over the same sets,
- and also polynomial or matrix rings over any
ring we can consider, including
polynomial or matrix rings themselves.
So we need infinitely many algebraic types.
Let us call these types RINGS.
Moreover we need ALGEBRAIC STRUCTURES
(ring, commutative ring, Euclidean domain,
field, finite field, prime field, univariate polynomial ring, ...)
for the following reasons.
- Genericity
- We can organize our infinitely many RINGS
in a finite number of RING types.
Then, for instance, we can define the Euclidean algorithm
once for all for every Euclidean domain.
For instance, for any Euclidean domain R we need to say
gcd(a,b) ==
while not zero? b repeat
(a,b):= (b,a rem b)
return a
- Conditional declaration
- A matrix ring (or polynomial ring) may possess
an operation (inverse, gcd, ...) that another does not
and this fact depends on its coefficient ring.
So our MATRIX RINGS and POLYNOMIAL RINGS
should depend on the properties of their coefficient RING.
For instance we need to say:
if R is a field then the ring R[x] of univariate
polynomials over R is an Euclidean domain.
- Conditional implementation
- The implementation of an operation defined
in several univariate polynomial rings like
(p, n)  pn pn |
(28) |
may depend on the properties of the coefficient RING.
Let R be a ring and
p(X) = aX + b
be a univariate polynomial in X with coefficient a, b
in R.
If R is a non-commutative ring then
| (aX + b)3 = a3X3 + (a2b + aba + ba2)X2 + (abb + bba + bab)X + b3. |
(29) |
If R is any commutative ring then
| (aX + b)3 = a3X3 + 3 a2bX2 + 3 ab2X + b3. |
(30) |
If R is
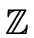 /3
/3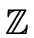 then
then
| (aX + b)3 = a3X3 + b3. |
(31) |
- Specialization
- Among all RINGS of a given type one
may have a much better algorithm for a given RING.
So for this particular one, we may wish to replace
the generic definition of an operation.
For instance for the Euclidean domain
of the integers we may wish to say (with some
optimizations ...)
gcd(a,b) ==
while a ~= b repeat
if a < b then b := b-a else a := a-b
return a


Next: How to encode the elements
Up: Implementing Computer Algebra: basic ideas
Previous: Implementing Computer Algebra: basic ideas
Marc Moreno Maza
2003-06-06
 pn
pn