Next: Modular inverses using Newton iteration Up: Division with remainder using Newton Previous: Classical division with remainder
We shall see now that the complexity result
of Proposition 1
can be improved.
To do so, we will show that ![]() can be computed from
can be computed from ![]() and
and ![]() by performing essentially one multiplication in
by performing essentially one multiplication in ![$ R[x]$](img5.png) .
We start with the equation
.
We start with the equation
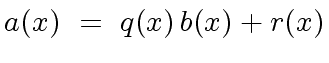 |
(2) |
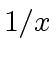 and multiplying the equation by
and multiplying the equation by 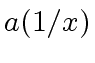 ,
, 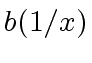 ,
, 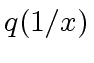 and
and 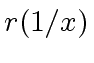 is multiplied by
is multiplied by ![$ R[x]$](img5.png) .
Definition 1 and
Proposition 2
highlight this fact.
Then
Proposition 3
and
Theorem 1
suggest Algorithm 2
which provides an efficient way to compute the inverse
of a univariate polynomial in
.
Definition 1 and
Proposition 2
highlight this fact.
Then
Proposition 3
and
Theorem 1
suggest Algorithm 2
which provides an efficient way to compute the inverse
of a univariate polynomial in
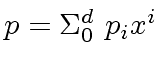 in
in ![$ R[x]$](img5.png) with degree
with degree 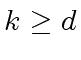 , the reversal of order
, the reversal of order 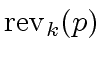 and defined by
and defined by
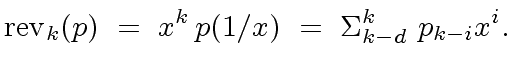 |
(4) |
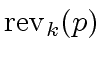 is simply denoted by
is simply denoted by
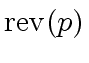 .
Hence we have
.
Hence we have
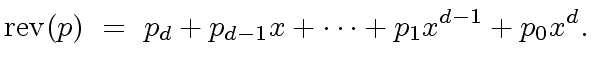 |
(5) |
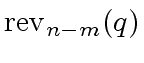 is invertible
modulo
is invertible
modulo 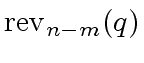 has constant coefficient
has constant coefficient 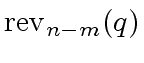 and
and Marc Moreno Maza