Next: A Probabilistic Approach Up: Computing primitive -th roots of Previous: Some results from group theory
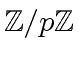 then the set
then the set
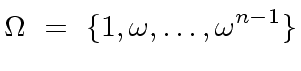 |
(42) |
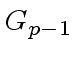 of
of
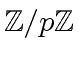 .
By vertue of Lagrange's theorem (Theorem 5)
the cardinality of
.
By vertue of Lagrange's theorem (Theorem 5)
the cardinality of 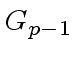 .
Since
.
Since 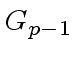 has
has 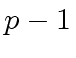 elements,
elements, 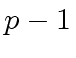 .
.
Conversly, it is known from finite field theory that 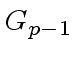 is a cyclic
group (even if
is a cyclic
group (even if ![]() is a power of a prime rather than a prime).
Let
is a power of a prime rather than a prime).
Let ![]() be a generator of this group, that is
be a generator of this group, that is
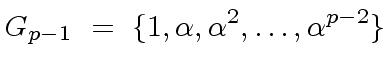 |
(43) |
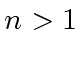 be an integer dividing
be an integer dividing 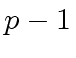 and define
and define
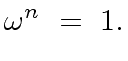 |
(45) |
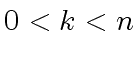 we have
we have
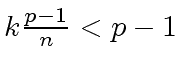 so
we have
so
we have
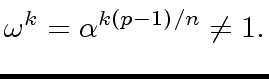 |
(46) |
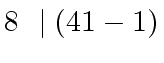 in
in
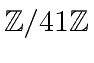 we have primitive
we have primitive 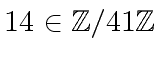 is such a root of unity.
is such a root of unity.
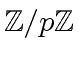 .
But this does not give an algorithm to construct them.
.
But this does not give an algorithm to construct them.
We could use brute force. Given
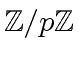 ,
for every
,
for every ![]() that we are interested in,
for every
that we are interested in,
for every
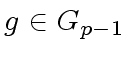 try if the following both statements hold:
try if the following both statements hold:
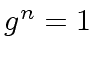 ,
,
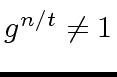 .
.
However we can reduce the complexity of this search by
computing a generator of 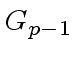 by means of
Theorem 7 and then applying
Relation (44).
by means of
Theorem 7 and then applying
Relation (44).
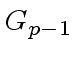 of the prime finite field
of the prime finite field
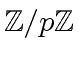 is a generator of
is a generator of 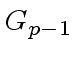 iff for every prime factor
iff for every prime factor 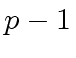 we have
we have
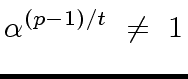 |
(47) |
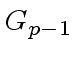 .
Then there exists an integer
.
Then there exists an integer 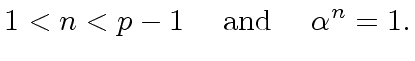 |
(48) |
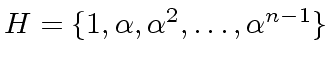 is a subgroup of
is a subgroup of 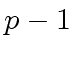 .
If
.
If 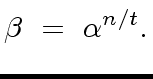 |
(49) |
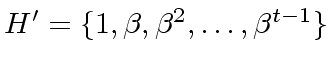 is a subgroup of
is a subgroup of
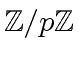 we are interested in primes
we are interested in primes 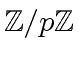 possesses a primitive
possesses a primitive 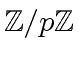 has such a root if there exists
has such a root if there exists
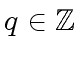 such that
such that
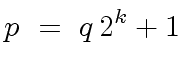 |
(50) |
But not all numbers of the form
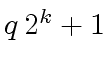 are prime
(consider
are prime
(consider 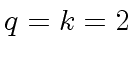 ).
So how frequent are the primes among the numbers
of the form
).
So how frequent are the primes among the numbers
of the form
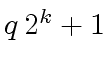 (for a given
(for a given ![]() ).
The answer is giving by the following theorem.
).
The answer is giving by the following theorem.
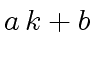 for
for
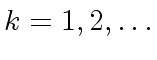
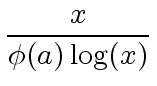 |
(51) |
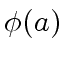 is the Euler function at
is the Euler function at
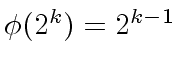 .
Therefore there are approximatively
.
Therefore there are approximatively
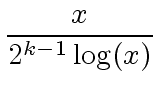 |
(52) |
Let
![]() , which represents the usual size
required for single precision integers.
For
, which represents the usual size
required for single precision integers.
For ![]() , there are approximatively 130
Fourier primes
, there are approximatively 130
Fourier primes
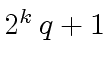 ,
,
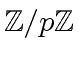 such that
such that
![$ {\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}[x]$](img298.png) whose product is of degree less than
whose product is of degree less than
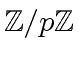 .
.
In the BasicMath library, one of the parents of libalgebra, nice primes are organized in tables. So there is a category for tables of primes!
macro SI == SingleInteger;
PrimesTableCategory(s: SI): Category == with {
sizeBound: () -> SI;
tableSize: () -> SI;
rank: SI -> Partial(SI);
maxPrime: () -> SI;
minPrime: () -> SI;
previousPrime: SI -> SI;
nextPrime: SI -> SI;
primes: () -> Generator(SI);
FourierDegree: SI -> SI;
getPrimeOfFourierDegree: SI -> SI;
nextPrimeOfFourierDegree: (SI, SI) -> SI;
unitsGenerator: SI -> SI;
primitiveRootofUnity: (SI, SI) -> SI;
}
where
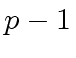 .
.
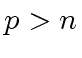 hold, otherwise 0
is returned.
hold, otherwise 0
is returned.
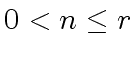 where
where
macro SI == SingleInteger;
FourierPrimesTableCategory(r: SI, s: SI): Category == with {
FourierDegree: () -> SI
sizeBound: () -> SI
tableSize: () -> SI
rank: SI -> Partial(SI)
maxPrime: () -> SI
minPrime: () -> SI
previousPrime: SI -> SI
nextPrime: SI -> SI
primes: () -> Generator(SI)
unitsGenerator: SI -> SI
primitiveRootofUnity: (SI, SI) -> SI
}
whereFourierPrimesTableCategory(r,s) specifies the operations that
we expect from the table of Fourier primes 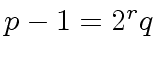 .
Again we restrict to primes that fit in a machine word.
.
Again we restrict to primes that fit in a machine word.
F6P15: FourierPrimesTableCategory(6,15) == add {
local fd: SI == 6;
local sb: SI == 15;
--------------------------------------------------------------------
-- Table (6,15) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^6
-- Number of 6-Fourier primes less than 2^15 is 58
MAXINDEX: SingleInteger == 58;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[193, 449, 577, 1217, 1601, 2113, 2753, 3137,
4289, 4673, 4801, 5441, 5569, 5953, 6337, 6977,
7489, 7873, 8513, 8641, 9281, 10177, 10433, 11329,
11969, 12097, 13121, 13249, 13633, 14401, 14657, 15809,
15937, 16193, 17729, 19009, 19777, 20161, 20929, 21313,
21569, 22721, 23873, 24001, 25153, 25409, 25537, 25793,
26177, 26561, 27073, 27329, 27457, 28097, 29633, 29761,
30529, 32321];
-- The corresponding units generators are:
local generatorList: Array SingleInteger :=
[5, 3, 5, 3, 3, 5, 3, 3,
3, 3, 7, 3, 13, 7, 10, 3,
7, 5, 5, 17, 3, 7, 3, 7,
3, 5, 7, 7, 5, 11, 3, 3,
7, 5, 3, 23, 11, 13, 7, 5,
3, 3, 3, 14, 10, 3, 10, 3,
3, 3, 5, 3, 7, 3, 3, 17,
13, 6];
FourierDegree(): SI == fd;
sizeBound(): SI == sb;
tableSize(): SI == MAXINDEX;
..............................................
}
F7P15: FourierPrimesTableCategory(7,15) == add {
local fd: SI == 7;
local sb: SI == 15;
--------------------------------------------------------------------
-- Table (7,15) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^7
-- Number of 7-Fourier primes less than 2^15 is 29
MAXINDEX: SingleInteger == 29;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[641, 1153, 1409, 2689, 3457, 4481, 4993, 6529,
7297, 9601, 9857, 10369, 11393, 12161, 13441, 13697,
15233, 16001, 18049, 19073, 19841, 20353, 21121, 21377,
26497, 28289, 29569, 30593, 31873];
-- The corresponding units generators are:
local generatorList: Array SingleInteger :=
[3, 5, 3, 19, 7, 3, 5, 7,
5, 13, 5, 13, 3, 3, 11, 3,
3, 3, 13, 3, 3, 5, 19, 3,
5, 6, 17, 3, 11];
FourierDegree(): SI == fd;
sizeBound(): SI == sb;
tableSize(): SI == MAXINDEX;
...........................................................
F8P15: FourierPrimesTableCategory(8,15) == add {
local fd: SI == 8;
local sb: SI == 15;
--------------------------------------------------------------------
-- Table (8,15) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^8
-- Number of 8-Fourier primes less than 2^15 is 12
MAXINDEX: SingleInteger == 12;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[257, 769, 3329, 7937, 9473, 14081, 14593, 22273,
23297, 26881, 30977, 31489];
-- The corresponding units generators are:
local generatorList: Array SingleInteger :=
[3, 11, 3, 3, 3, 3, 5, 5,
3, 11, 3, 7];
FourierDegree(): SI == fd;
sizeBound(): SI == sb;
tableSize(): SI == MAXINDEX;
...........................................................
9P23: FourierPrimesTableCategory(9,23) == add {
local fd: SI == 9;
local sb: SI == 23;
--------------------------------------------------------------------
-- Table (9,23) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^9
-- Number of 9-Fourier primes less than 2^23 is 1092
MAXINDEX: SingleInteger == 1092;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[7681, 10753, 11777, 17921, 23041, 26113, 32257,
...........................................................
F10P24: FourierPrimesTableCategory(10,24) == add {
local fd: SI == 10;
local sb: SI == 24;
--------------------------------------------------------------------
-- Table (10,24) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^10
-- Number of 10-Fourier primes less than 2^24 is 1087
MAXINDEX: SingleInteger == 1087;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[13313, 15361, 19457, 25601,
...........................................................
F11P25: FourierPrimesTableCategory(11,25) == add {
local fd: SI == 11;
local sb: SI == 25;
--------------------------------------------------------------------
-- Table (11,25) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^11
-- Number of 11-Fourier primes less than 2^25 is 978
MAXINDEX: SingleInteger == 978;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[18433,
...........................................................
F12P26: FourierPrimesTableCategory(12,26) == add {
local fd: SI == 12;
local sb: SI == 26;
--------------------------------------------------------------------
-- Table (12,26) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^12
-- Number of 12-Fourier primes less than 2^26 is 972
MAXINDEX: SingleInteger == 972;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[12289,
...........................................................
Marc Moreno Maza