Next: Bibliography Up: Foundations of Computer Algebra: Hensel Previous: Linear Hensel Lifting
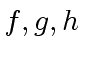 be univariate polynomials in
be univariate polynomials in ![$ R[x]$](img50.png) and let
and let 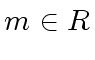 .
We assume that the following relation holds
.
We assume that the following relation holds
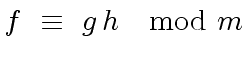 |
(26) |
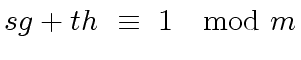 |
(28) |
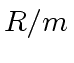 is a field then we can compute
is a field then we can compute ![$ R[x]/m$](img107.png) .
.
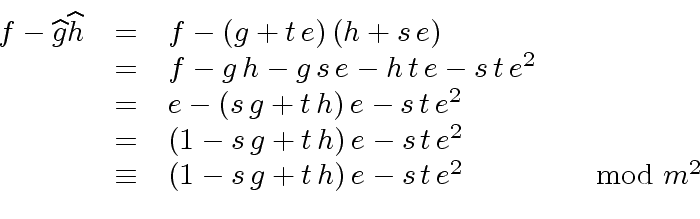 |
(30) |
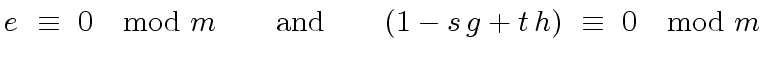 |
(31) |
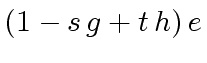 and
and 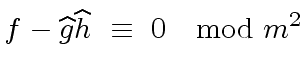 |
(32) |
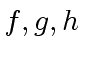 are constants of
are constants of 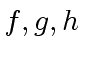 do not need to be polynomials!
The factorization lifting problem and its solution
by Proposition 1
are valid in any commutative ring with identity element.
But for this solution to be an algorithm
one needs to be able to compute the Bézout coefficients
do not need to be polynomials!
The factorization lifting problem and its solution
by Proposition 1
are valid in any commutative ring with identity element.
But for this solution to be an algorithm
one needs to be able to compute the Bézout coefficients
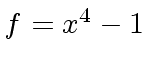 ,
, 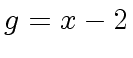 ,
,
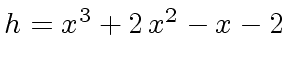 and
and
N := NonNegativeInteger
(1) NonNegativeInteger
Type: Domain
Z := Integer
(2) Integer
Type: Domain
U := UnivariatePolynomial(x,Z)
(3) UnivariatePolynomial(x,Integer)
Type: Domain
m: Z := 5
(4) 5
Type: Integer
f: U := x^4 - 1
4
(5) x - 1
Type: UnivariatePolynomial(x,Integer)
g: U := x - 2
(6) x - 2
Type: UnivariatePolynomial(x,Integer)
h: U := x^3 + 2 *x^2 -x -2
3 2
(7) x + 2x - x - 2
Type: UnivariatePolynomial(x,Integer)
e := f - g*h
2
(8) 5x - 5
Type: UnivariatePolynomial(x,Integer)
K5 := PrimeField(5)
(9) PrimeField
Type: Domain
U5 := UnivariatePolynomial(x,K5)
(10) UnivariatePolynomial(x,PrimeField 5)
Type: Domain
f5: U5 := f :: U5
4
(11) x + 4
Type: UnivariatePolynomial(x,PrimeField 5)
g5: U5 := g :: U5
(12) x + 3
Type: UnivariatePolynomial(x,PrimeField 5)
h5: U5 := h ::U5
3 2
(13) x + 2x + 4x + 3
Type: UnivariatePolynomial(x,PrimeField 5)
res := extendedEuclidean(g5,h5)
2
(14) [coef1= 2x + 3x + 4,coef2= 3,generator= 1]
s5: U5 := res.coef1
2
(15) 2x + 3x + 4
Type: UnivariatePolynomial(x,PrimeField 5)
t5: U5 := res.coef2
(16) 3
Type: UnivariatePolynomial(x,PrimeField 5)
g_^ := g + t5 :: U * e
2
(17) 15x + x - 17
Type: UnivariatePolynomial(x,Integer)
h_^ := h + s5 :: U * e
4 3 2
(18) 10x + 16x + 12x - 16x - 22
Type: UnivariatePolynomial(x,Integer)
factor(f - g_^ * h_^ )
4 3 2
(19) - 25(x - 1)(x + 1)(6x + 10x + 7x - 10x - 15)
Type: Factored UnivariatePolynomial(x,Integer)
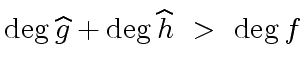 |
(33) |
![$ R[x]$](img50.png) .
We will take advantage of the following.
.
We will take advantage of the following.
![$ R[x]$](img50.png) such that
such that 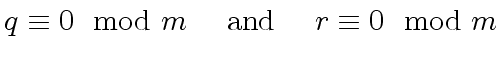 |
(34) |
![$ a^{\ast} \in R[x]$](img123.png) such that
such that
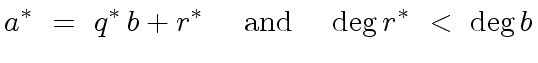 |
(35) |
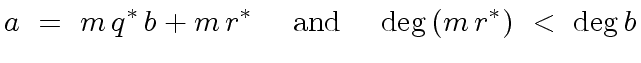 |
(36) |
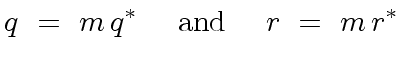 |
(37) |
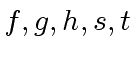 be polynomials in
be polynomials in ![$ R[x]$](img50.png) and let
and let 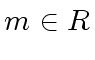 .
We say that
.
We say that
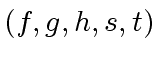 is a liftable quintet modulo
is a liftable quintet modulo 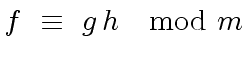 ,
,
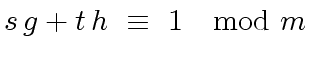 ,
,
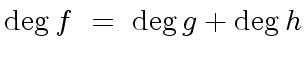 ,
,
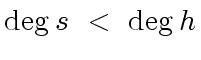 ,
,
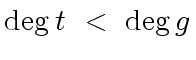 .
.
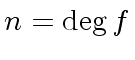 .
If
.
If
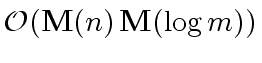 word operations.
word operations.
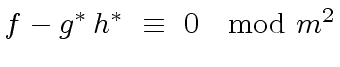 ,
,
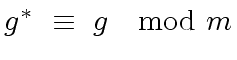 ,
,
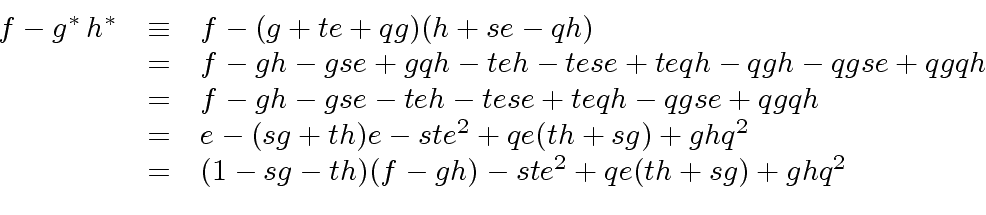 |
(38) |
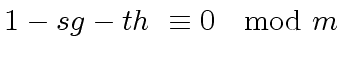
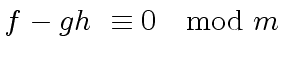
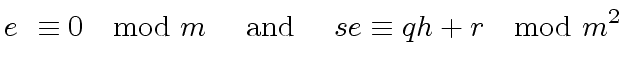 |
(39) |
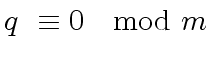 |
(40) |
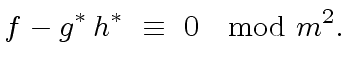 |
(41) |
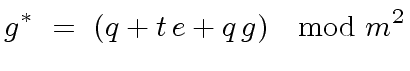 |
(42) |
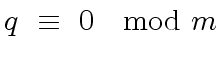 imply
imply
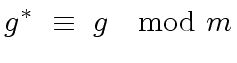 |
(43) |
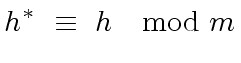 |
(44) |
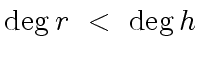 |
(45) |
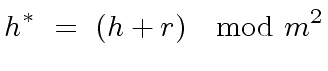 |
(46) |
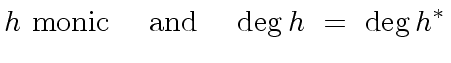 |
(47) |
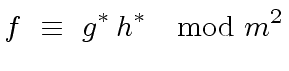 |
(48) |
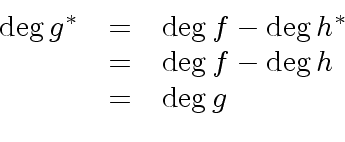 |
(49) |
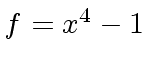 ,
, 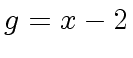 ,
,
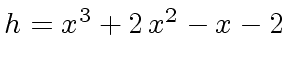 and
and 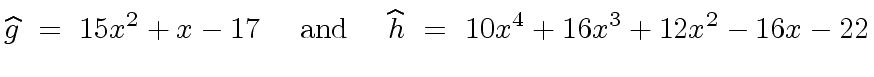 |
(50) |
N := NonNegativeInteger
(1) NonNegativeInteger
Type: Domain
Z := Integer
(2) Integer
Type: Domain
U := UnivariatePolynomial(x,Z)
(3) UnivariatePolynomial(x,Integer)
Type: Domain
m: Z := 5
(4) 5
Type: Integer
f: U := x^4 - 1
4
(5) x - 1
Type: UnivariatePolynomial(x,Integer)
g: U := x - 2
(6) x - 2
Type: UnivariatePolynomial(x,Integer)
h: U := x^3 + 2 *x^2 -x -2
3 2
(7) x + 2x - x - 2
Type: UnivariatePolynomial(x,Integer)
e := f - g*h
2
(8) 5x - 5
Type: UnivariatePolynomial(x,Integer)
K5 := PrimeField(5)
(9) PrimeField 5
Type: Domain
U5 := UnivariatePolynomial(x,K5)
(10) UnivariatePolynomial(x,PrimeField 5)
Type: Domain
f5: U5 := f :: U5
4
(11) x + 4
Type: UnivariatePolynomial(x,PrimeField 5)
g5: U5 := g :: U5
(12) x + 3
Type: UnivariatePolynomial(x,PrimeField 5)
h5: U5 := h ::U5
3 2
(13) x + 2x + 4x + 3
Type: UnivariatePolynomial(x,PrimeField 5)
res := extendedEuclidean(g5,h5)
2
(14) [coef1= 2x + 3x + 4,coef2= 3,generator= 1]
Type: Record(coef1: UnivariatePolynomial(x,PrimeField 5),
coef2: UnivariatePolynomial(x,PrimeField 5),
generator: UnivariatePolynomial(x,PrimeField 5))
s5: U5 := res.coef1
2
(15) 2x + 3x + 4
Type: UnivariatePolynomial(x,PrimeField 5)
s: U := s5 :: U
2
(16) 2x + 3x + 4
Type: UnivariatePolynomial(x,Integer)
t5: U5 := res.coef2
(17) 3
Type: UnivariatePolynomial(x,PrimeField 5)
t: U := t5 :: U
(18) 3
Type: UnivariatePolynomial(x,Integer)
R25 := IntegerMod(25)
(19) IntegerMod 25
Type: Domain
U25 := UnivariatePolynomial(x,R25)
(20) UnivariatePolynomial(x,IntegerMod 25)
Type: Domain
e25 := f::U25 - g::U25 * h::U25
2
(21) 5x + 20
Type: UnivariatePolynomial(x,IntegerMod 25)
e : U := e25 :: U
2
(22) 5x + 20
Type: UnivariatePolynomial(x,Integer)
res := monicDivide(s*e, h)
2
(23) [quotient= 10x - 5,remainder= 80x + 75x + 70]
Type: Record(quotient: UnivariatePolynomial(x,Integer),
remainder: UnivariatePolynomial(x,Integer))
q25: U25 := res.quotient :: U25
(24) 10x + 20
Type: UnivariatePolynomial(x,IntegerMod 25)
r25: U25 := res.remainder :: U25
2
(25) 5x + 20
Type: UnivariatePolynomial(x,IntegerMod 25)
g_* := (g::U25 + t::U25 * e25 + q25 * (g::U25)) :: U
(26) x + 18
Type: UnivariatePolynomial(x,Integer)
h_* := (h::U25 + r25) :: U
3 2
(27) x + 7x + 24x + 18
Type: UnivariatePolynomial(x,Integer)
(f - g_* * h_*) :: U25
(28) 0
Type: UnivariatePolynomial(x,IntegerMod 25)
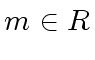 which is not a zero divisor, an integer
which is not a zero divisor, an integer
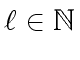 and nonzero univariate polynomials
and nonzero univariate polynomials
![$ g, h, g^{\ast}, h^{\ast}, s, t \in R[x]$](img165.png) such that
such that
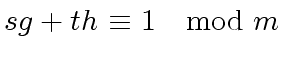
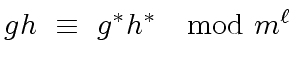
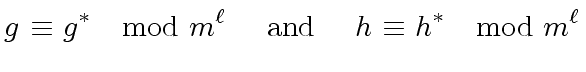 |
(51) |
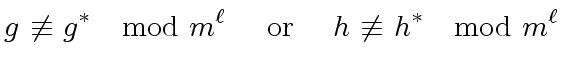 |
(52) |
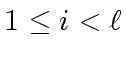 be maximal such that
be maximal such that
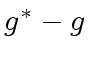 and
and
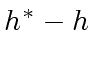 .
Thus there exist polynomials
.
Thus there exist polynomials
![$ u, v \in R[x]$](img174.png) such that
such that
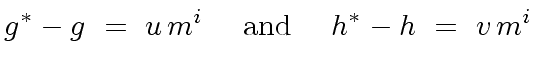 |
(53) |
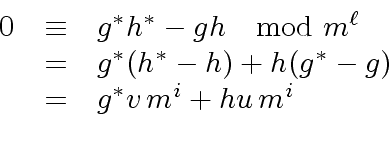 |
(54) |
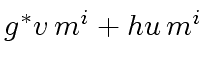 .
In other words there exist
.
In other words there exist
![$ w \in R[x]$](img179.png) such that
such that
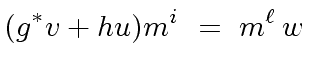 |
(55) |
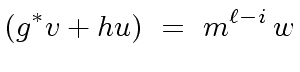 |
(56) |
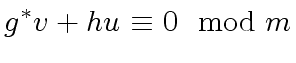 |
(57) |
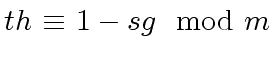 |
(58) |
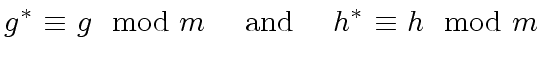 |
(59) |
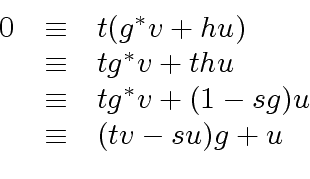 |
(60) |
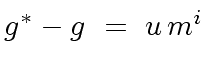 together with the facts that
together with the facts that 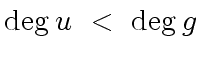 |
(61) |
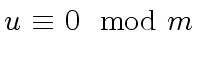 |
(62) |
Marc Moreno Maza