Efficiency

In any MONOID exponentiation can de defined by the binary powering algorithm

        (^)(x: %, n: NonNegativeInteger): % ==
                (n < 0) =>
                        error "power:  negative exponent";
                n = 0 => 1;
                n = 1 => x;
                n = 2 => x*x;

                -- General code.
                i: SingleInteger := 0;
                l: SingleInteger := length n;
                u: % := 1;
                repeat {
                        if bit(n, i) then u := u * x;
                        if i >= l then break;
                        x := x * x;
                        i := i + 1;
                }
                u
        }

Assume that in the interface MONOID the exponentiation has been defined as above. In the MONOID 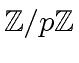${\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}$ (where 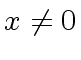$p$ is a prime) we can do better because of little Fermat theorem which states that for $x \neq 0$ we have 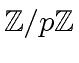$x^{p-1} = 1$ . Hence we need to overwrite the above definition for ${\mbox{${\mathbb{Z}}$}}/p{\mbox{${\mathbb{Z}}$}}$ by something like

        (^)(x: %, n: NonNegativeInteger): % == {
            n := positiveRemainder(n,p);
            zero? n => 1;
            one? x => x;
            local acc: %;
            if odd? n then acc := x else acc := 1;
            repeat {
                n := shift(n,-1);
                zero? n => return acc;
                x := (x * x) mod p;
                if odd? n then acc := (acc * x) mod p;
            }
        }

This will be made possible by INHERITANCE. In a polynomial ring $R[x]$ one can do better too in some special cases depending on the coefficient ring, as we have seen before. This will be made possible by CONDITIONAL IMPLEMENTATION.