Challenges and Achievements

The main challenges of symbolic/exact computations:

• intermediate expression swell,
• complexity of symbolic computations
• implementing fast algorithms.

We iluustrate below the gap between naive and optimized implementations of the same algorithm.

Figure: Polynomial addition over ${\mbox{${\mathbb Z}$}}/p{\mbox{${\mathbb Z}$}}$ .

Figure: Polynomial multiplication over ${\mbox{${\mathbb Z}$}}/p{\mbox{${\mathbb Z}$}}$ .

Next, we show benchmarks between classical and FFT-based univariate polynomial multiplication.

Figure: FFT-based univariate polynomial multiplication over ${\mbox{${\mathbb Z}$}}/p{\mbox{${\mathbb Z}$}}$

Figure: Classical vs FFT-based univariate polynomial multiplication over ${\mbox{${\mathbb Z}$}}/p{\mbox{${\mathbb Z}$}}$

The maple work sheet Bareiss.mw iluustrates the problem of intermediate expression swell. In many situations, this problem is solved by means of modular methods. Here's an example of such method that will study in detail later

Input:

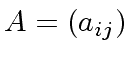$A=(a_{ij})$ a square matrix over 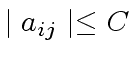${\mbox{${\mathbb{Z}}$}}$ of order $n$ with $\mid a_{ij} \mid \leq C$ for $1 \leq i,j \leq n$ .

Output:

${\det}(A) \in {\mbox{${\mathbb{Z}}$}}$ .

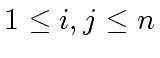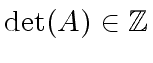Another example of intermediate expression swell is given below. Consider the polynomials

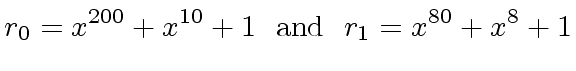$$r_0 = {x \sp {200}}+{x \sp {10}}+1 \ \ {\rm and } \ \ r_1 = {x \sp {80}}+{x \sp 8}+1$$ (1)

in the ring ${\mbox{${\mathbb{Q}}$}}[x]$ . The successive remainders of the Euclidean Algorithm applied to $r_0$ and $r_1$ are

• $r_2 = {x \sp {56}}+{2 \ {x \sp {48}}}+{x \sp {40}}+{x \sp {10}}+1$
• $r_3 = {5 \ {x \sp {48}}}+{4 \ {x \sp {40}}} -{x \sp {34}}+{2 \ {x \sp {26}}} -... ... -{3 \ {x \sp {18}}}+{2 \ {x \sp {16}}}+{4 \ {x \sp {10}}} -{2 \ {x \sp 8}}+5$
• $r_4 = {{1 \over 5} \ {x \sp {42}}}+{{1 \over {25}} \ {x \sp {40}}} -{{4 \over ... ...+{{1 \over {25}} \ {x \sp {10}}} -{{{13} \over {25}} \ {x \sp 8}} -{1 \over 5}$
• $r_5 = {{{1001} \over {625}} \ {x \sp {40}}} -{{{29} \over {25}} \ {x \sp {38}... ...} -{{1 \over 5} \ {x \sp 4}}+{{1 \over {25}} \ {x \sp 2}}+{{124} \over {125}}$
• $r_6 = {{{525625} \over {1002001}} \ {x \sp {38}}}+{{{20000} \over {1002001}} \... ...sp 4}} -{{{643750} \over {1002001}} \ {x \sp 2}} -{{1575625} \over {1002001}}$
• $r_7 = {{{511511} \over {707281}} \ {x \sp {36}}} -{{{1439438} \over {707281}} ... ... \sp 4}}+{{{1477476} \over {707281}} \ {x \sp 2}} -{{1178177} \over {707281}}$
• $r_8 = {{{1396901} \over {261121}} \ {x \sp {34}}} -{{{1306073} \over {261121}}... ...{x \sp 4}} -{{{1869543} \over {261121}} \ {x \sp 2}}+{{932669} \over {261121}}$
• $r_9 = {{{1451751} \over {2758921}} \ {x \sp {32}}}+{{{785918} \over {2758921}}... ...\sp 4}} -{{{811468} \over {2758921}} \ {x \sp 2}} -{{2893282} \over {2758921}}$
• $r_{10} = {{{2444992} \over {8071281}} \ {x \sp {30}}}+{{{2089538} \over {80712... ...p 4}} -{{{1376969} \over {8071281}} \ {x \sp 2}} -{{18359033} \over {8071281}}$
• $r_{11} = {{{821049} \over {541696}} \ {x \sp {28}}}+{{{1230153} \over {135424... ...\sp 4}}+{{{7338303} \over {1083392}} \ {x \sp 2}} -{{4707537} \over {1083392}}$
• $r_{12} = {{{2879600} \over {83521}} \ {x \sp {26}}} -{{{2819432} \over {83521}... ... {x \sp 4}}+{{{2110296} \over {83521}} \ {x \sp 2}} -{{1857480} \over {83521}}$
• $r_{13} = {{{489294629} \over {244922500}} \ {x \sp {24}}} -{{{84853001} \over ... ...4}}+{{{1074213} \over {244922500}} \ {x \sp 2}}+{{79874687} \over {48984500}}$
• $r_{14} = {{{101577545700} \over {2866455549721}} \ {x \sp {22}}}+{{{3670763840... ...800} \over {2866455549721}} \ {x \sp 2}}+{{36036190800} \over {2866455549721}}$
• $r_{15} ={{{179398565293636} \over {10531900693521}} \ {x \sp {20}}} -{{{54943... ... \over {10531900693521}} \ {x \sp 2}}+{{2527399767739} \over {1170211188169}}$
• $r_{16} = {{{2517066778702173} \over {11227749627077776}} \ {x \sp {18}}} -{{{... ...227749627077776}} \ {x \sp 2}} -{{2469351761856789} \over {11227749627077776}}$
• $r_{17} = {{{849182055193466800} \over {601565221018811449}} \ {x \sp {16}}}+{... ...221018811449}} \ {x \sp 2}}+{{429248529314696936} \over {601565221018811449}}$
• $r_{18} = {{{8093646079436159529} \over {64225707449292490000}} \ {x \sp {14}}... ...292490000}} \ {x \sp 2}} -{{311063035823698661} \over {32112853724646245000}}$
• $r_{19} = -{{{321061300213427783600} \over {108894438325788541209}} \ {x \sp {... ...6180403}} \ {x \sp 2}}+{{49162422013935572500} \over {108894438325788541209}}$
• $r_{20} = {{{4829115100553781731631} \over {401242596572878762276}} \ {x \sp {1... ...524552}} \ {x \sp 2}}+{{373138984504746247389} \over {802485193145757524552}}$
• $r_{21} = -{{{37302462364041459452987} \over {214155589697125984393929}} \ {x \... ...8}} \ {x \sp 2}} -{{34803628802314892079373} \over {428311179394251968787858}}$
• $r_{22} = {{{1062516113981431489446399} \over {55486579353465726911265604}} \ {... ...\ {x \sp 2}}+{{13859935515210895384665945} \over {55486579353465726911265604}}$
• $r_{23} = {{{67553029541578289076276832} \over {5271590127845040063150969}} \ {... ... {x \sp 2}} -{{117836407258993771969728352} \over {5271590127845040063150969}}$
• $r_{24} = -{{{144893287293662194035293991} \over {20560880907683469568857664}} \ {x \sp 2}}+{{23864545606303620039559371} \over {2570110113460433696107208}}$
• $r_{25} = {{1474954192646018616432640872} \over {3982491846600722083699067449}}$
• $r_{26} = 0$

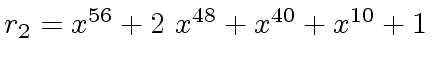
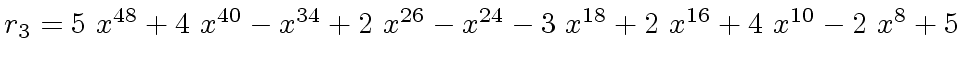
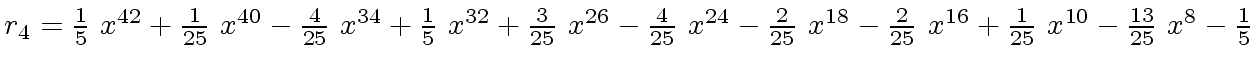
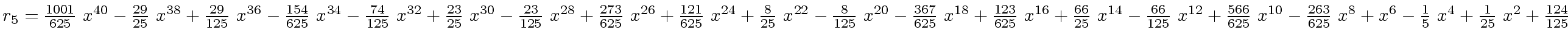
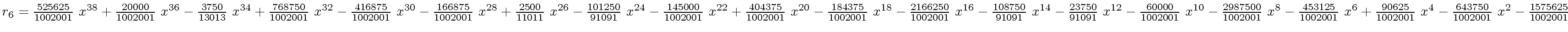
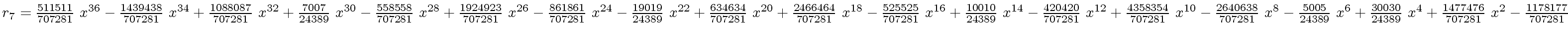
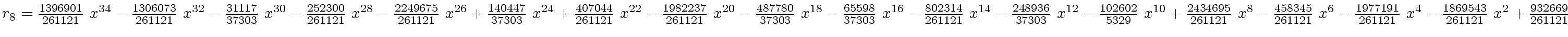
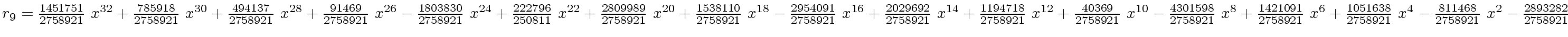
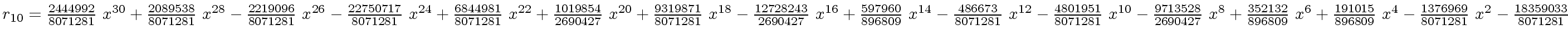
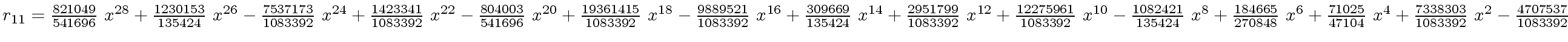
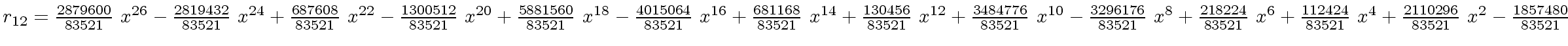
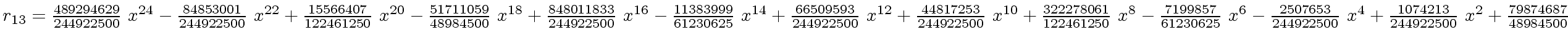
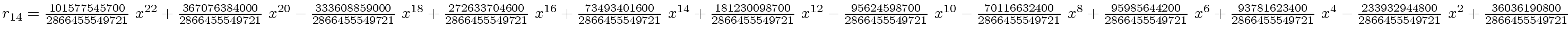
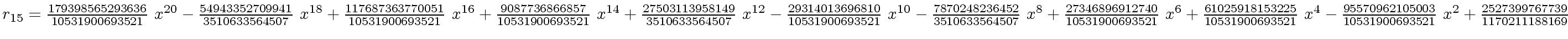
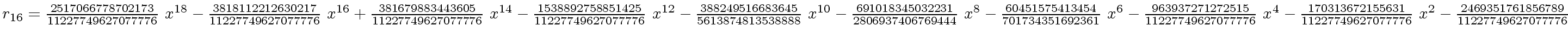
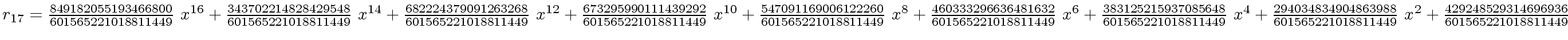
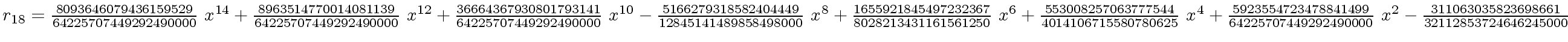
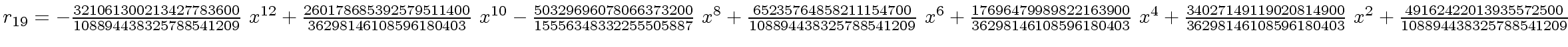
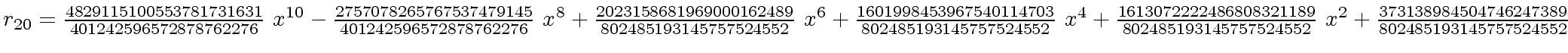
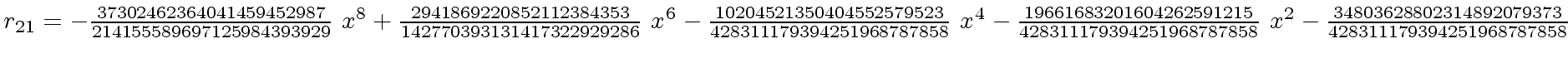
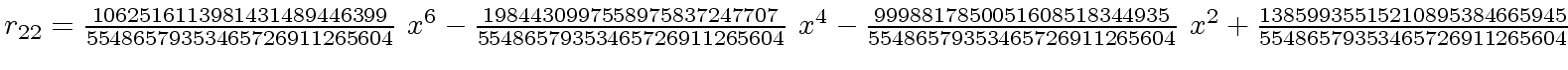
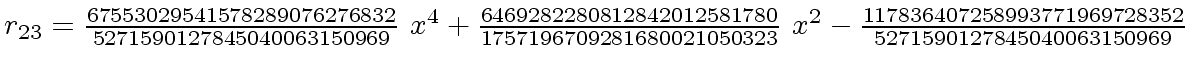
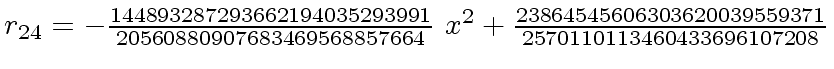
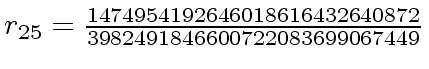
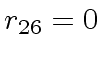
We will study modular methods for the Euclidean Algorithm too.