Remark 7
The above remarks and proposition lead us to the following
ALDOR implementation of the residue class ring of an Euclidean
domain R
mathend000# by one of its element.
ResidueClassRing(R:EuclideanDomain, p:R): Ring with {
class: R -> %;
sample: % -> R;
} == R add {
Rep == R;
import from R;
1: % == per(1);
0: % == per(0);
zero?(x:%): Boolean == zero?(rep(x));
(x:%) = (y:%) : Boolean == zero?(x-y);
one?(x:%): Boolean == x = 1;
class(a:R):% == {
(q,r) := divide(a,p);
per(r);
}
sample(x:%): R == rep(x);
(x:%) + (y:%) : % == class(rep(x) + rep(y));
-(x:%) : % == class(-rep(x));
(x:%) * (y:%) : % == class(rep(x) * rep(y));
(n:Integer) * (x:%): % == class(n * rep(x));
(x:%) ^ (n:NonNegativeInteger) : % == class(rep(x) ^ n);
recip(x:%): Partial(%) == {
import from Partial(%);
(u,v,g) := extendedEuclidean(rep(x),p);
h?: Partial(R) := recip(g);
failed? h? => failed();
h: R := retract(h?);
[class(h * u)];
}
}
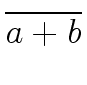 and
and  p | (qa - qb)p + ra - rb
p | (qa - qb)p + ra - rb  p | ra - rb
p | ra - rb ra = rb
ra = rb a(u) = b(u)
a(u) = b(u)